Banda Möbius

În topologie , banda Möbius (numită și banda Möbius sau bucla Möbius ) este o suprafață compactă a cărei margine este homeomorfă pentru un cerc . Cu alte cuvinte, are o singură față, spre deosebire de o bandă convențională care are două. Suprafața are particularitatea de a fi reglată și nu orientabilă . A fost descris independent în 1858 de către matematicienii August Ferdinand Möbius (1790-1868) și Johann Benedict Listing (1808-1882). Numele primului a fost păstrat grație unei teze prezentate Academiei de Științe din Paris . De asemenea, găsim numele de „trupă”, „inel” sau „centură” a lui Möbius și uneori scriem „Mœbius” sau „Moebius”.

Este ușor să vizualizați banda Möbius în spațiu: un model simplu este realizat prin răsucirea unei benzi lungi de hârtie o jumătate de tură , apoi lipirea celor două capete împreună, creând o panglică interminabilă n 'care nu are nici interior, nici exterior.

Definiție prin torsiunea unei benzi în spațiu

• Plan de asamblare a panglicii

• Realizarea panglicii.

• Diagrama ansamblului: lipiți cele două săgeți înapoi respectând direcția.

Bandă clasică Möbius

Banda Möbius poate fi generată de un segment pivotant al cărui centru descrie un cerc fix. O setare corespunzătoare este

{X=(1+t2cos⁡v2)cos⁡vy=(1+t2cos⁡v2)păcat⁡vz=t2păcat⁡v2-1≤t≤10<v≤2π{\ displaystyle {\ begin {cases} x = (1 + {\ frac {t} {2}} \ cos {\ frac {v} {2}}) \ cos v \\ y = (1 + {\ frac {t} {2}} \ cos {\ frac {v} {2}}) \ sin v \\ z = {\ frac {t} {2}} \ sin {\ frac {v} {2}} \ end {cases}} \ qquad {\ begin {matrix} -1 \ leq t \ leq 1 \\ 0 <v \ leq 2 \ pi \ end {matrix}}}

sau setul de soluții ale următoarei ecuații:

X2y+yz2+y3-y-2Xz-2X2z-2y2z=0.{\ displaystyle x ^ {2} y + yz ^ {2} + y ^ {3} -y-2xz-2x ^ {2} z-2y ^ {2} z = 0.}

Curbele v = v 0 , t care variază singure, sunt într-adevăr segmente, conectând la viteză uniformă punctul v = v 0 , t = –1 și punctul v = v 0 , t = 1. Acest segment are deci lungimea 2.

Curba t = 0 este un cerc de diametru 2 în plan orizontal; reprezintă traiectoria centrului segmentelor. Unghiul pe care îl face segmentul cu direcția orizontală este v 0 . Când centrul a făcut o întoarcere completă pe cercul orizontal (adăugând π la variabila v ), segmentul a făcut doar o întoarcere în U. Acest lucru determină conexiunea de exemplu a punctului t = 1, v = π cu t = –1, v = 0.

Marginea benzii este dată de curba t = 1 sau t = –1. Dar este aceeași curbă: marginea benzii Möbius este într-o singură bucată ( conectată ).

De asemenea, putem vedea animația de mai sus în vederea stereoscopică  :

• Animație stereoscopică încrucișată:
• Animație stereoscopică paralelă a aceleiași benzi:

Alte cifre obținute prin torsiune

Variante ale benzii convenționale pot fi obținute prin supunerea pânzei de hârtie la un număr impar de jumătăți de întoarcere înainte sau înapoi. Tot ce trebuie să faceți este să reglați setarea anterioară:

{X=(2+tcos⁡kv)cos⁡2vy=(2+tcos⁡kv)păcat⁡2vz=tpăcat⁡kv-1≤t≤10<v≤π{\ displaystyle {\ begin {cases} x = (2 + t \ cos kv) \ cos 2v \\ y = (2 + t \ cos kv) \ sin 2v \\ z = t \ sin kv \ end {cases} } \ qquad {\ begin {matrix} -1 \ leq t \ leq 1 \\ 0 <v \ leq \ pi \ end {matrix}}}

cu k număr întreg relativ impar .

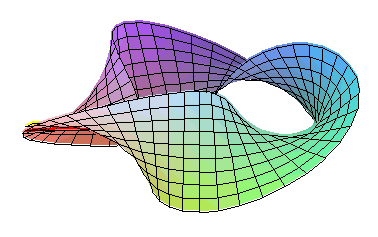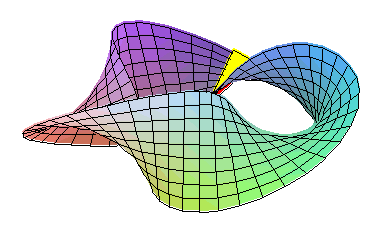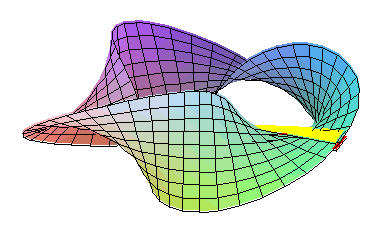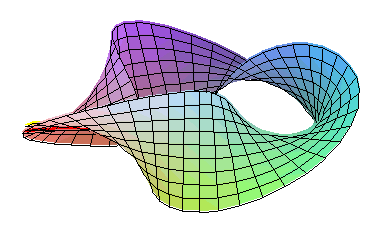
Cifrele obținute pentru k și - k sunt enantiomorfe , adică imagini oglindite una cu cealaltă.

Dacă se acceptă valori egale de k, se obțin benzi cu două fețe, mai mult sau mai puțin răsucite.

Compararea diferitelor panglici

Ne poate interesa curba care formează marginea acestor panglici. Are o îndoială diferită pentru fiecare valoare a lui k . Răsucirea este calculată de exemplu în proiecție (vedere de sus), numărând de câte ori curba trece peste ea însăși. Nu se poate deforma continuu (adică prin homotopie ) un tip de bandă într-un altul în spațiul tridimensional.

Cu toate acestea, diferitele panglici sunt homeomorfe față de banda clasică Möbius, adică nu există nicio diferență intrinsecă între ele. Acest lucru este legat de modul în care sunt scufundați în spațiul tridimensional.

Banda Möbius pe jumătate poate fi văzută și ca parte a suprafeței Möbius.

Obiecte derivate

Dacă lipim două panglici Möbius de-a lungul marginii lor, vom obține o sticlă Klein . Acest lucru poate fi realizat numai prin ruperea panglicii (sau prin utilizarea celei de-a patra dimensiuni), deoarece sticla Klein nu se scufundă în spațiul obișnuit.

Dacă lipim un disc pe o bandă Möbius de-a lungul marginii lor comune, obținem un plan proiectiv real  ; din nou, nu este posibil să faceți acest lucru fizic fără a rupe panglica.

Dacă încercăm să-l tăiem în trei, adică urmând o axă o treime din lățimea uneia dintre margini, obținem două panglici întrețesute: o bandă Möbius de o treime din lățime, corespunzătoare mijlocului de pornire panglică și o panglică față-verso cu o treime lată, care se potrivește cu marginea panglicii de pornire, dublă în lungime și răsucită cu o rotație completă.

Am văzut că, dacă tăiem o bandă Möbius de-a lungul axei mediane, obținem o bandă pe două fețe, răsucită și de lungime dublă. Dacă tăiem această panglică pe lungime, obținem două inele distincte, răsucite și împletite.

În cele din urmă, dacă începem cu o bandă Möbius obținută prin trei jumătăți de rotație înainte de lipire (precum cea din sigla de mai jos ) și o tăiem de-a lungul axei mediane, obținem o singură bandă, dar legată (într-un nod trifoliat ).

Alegerea lungimii panglicii

Banda Möbius poate fi produsă cu o bandă flexibilă a unei foi de hârtie de 70 g / m 2 , de exemplu. Pentru a obține o panglică fără pliere bruscă, este necesar ca, pentru o lățime a panglicii egală cu 1, lungimea să fie mai mare de 1,732 - adică rădăcina pătrată a lui 3. Este posibil să mergeți spre o lungime mai mică până la atingerea întâlniți, cu o inversare elicoidală, laturile opuse ale unui pătrat, dar coturile vor fi bruste.

Utilitatea panglicii

În timp ce Mobius poate apărea doar ca o curiozitate matematică sau ca o construcție artistică, această prevedere a fost adesea folosită în lumea industrială a  secolului al XIX- lea, când mașinile funcționau din curele. Centurile au fost încrucișate la joncțiune pentru a uza „ambele părți” ale centurii în același timp. De fapt, descrierea benzii Möbius va arăta că centura avea o singură parte.

Definiție prin identificare abstractă

Construcția de mai sus (prin lipirea unei benzi după răsucire cu o jumătate de tură) este formalizată spunând că banda Möbius este cartografierea torului homeomorfismului [–1, 1] → [–1, 1], x ↦ - x , adică spațiul de produs [-1, 1] × [0, 1] quotiented prin relația de echivalență ( x , 1) ~ (- x , 0). Obținem astfel un pachet de fibre [–1, 1] pe cercul S 1 .

Prin comparație, banda „normală” (trunchiul unui cilindru) corespunde homeomorfismului identitar al [–1, 1] și, prin urmare, pachetului banal , produsul [–1, 1] × S 1 .

Acest lucru vă permite să vedeți matematic ce se întâmplă atunci când tăiați banda: dacă p  : [–1, 1] × [0, 1] → ([–1, 1] × [0, 1]) / ∼ denotă aplicarea trecerea la coeficient, p ({0} × [0, 1]) este un cerc al cărui complement este conectat .

De asemenea, putem realiza banda Möbius ca complement al unui disc deschis în planul proiectiv real .

Reprezentări artistice

Banda Möbius apare în multe producții artistice.

Siglă

• O versiune schematică a benzii Möbius a fost utilizată ca simbol pentru reciclare încă de la prima Zi a Pământului din 1970 . Bucla Möbius indică faptul că un produs poate fi reciclat sau că a fost realizat din materiale reciclate. Este de fapt o panglică cu trei jumătăți de spire.
• O versiune a panglicii Möbius este utilizată ca logo pentru Visual Studio , instrumentul de dezvoltare IT al Microsoft .
• A devenit, de asemenea, sigla pentru Google Drive , serviciul online de stocare a datelor Google .
• El este, de asemenea, simbolul grupului K-pop Infinite .
• Logo-ul Léman Express , rețeaua regională expresă din regiunea Franco-Valdo-Geneva , are această panglică ca logo, care reprezintă aici Lacul Geneva .
• Logo-ul mărcii Renault este inspirat de o panglică Möbius.

Filme și seriale

• Moebius , film argentinian de science-fiction de Gustavo Mosquera R., lansat în 1996.
• Thru the Moebius Strip , un film complet digital de 80 de minute regizat de Frank Foster la Global Digital Productions (Hong Kong). Filmul a fost lansat în Statele Unite în 2005 .
• Panglica Möbius a fost folosită și în episodul Fotoliul uitării din desene animate Ulise 31 unde copiii protagonistului s-au trezit condamnați la o plimbare nesfârșită pe panglică.
• Moebius este, de asemenea, numele dublului episod final din sezonul 8 din Stargate SG-1 .
• Autostrada pierdută a lui David Lynch este adesea comparată cu o bandă Möbius. La începutul complotului, Fred Madison, din interiorul casei sale, primește un apel de interfon. Și în cele din urmă, el însuși, cel din afara casei, vorbește în interfon, la fel pentru Timecrimes .
• În seria Awake , mintea detectivului Michael Britten este considerată o panglică Möbius de către unul dintre psihanaliști.
• În 2013 , un film de spionaj regizat de Eric Rochant ( Les Patriotes ), cu Jean Dujardin și Cécile de France , a fost intitulat Möbius .
• Într-un episod din Futurama , D r Farnsworth a alergat împotriva Leelei pe o pistă în formă de Mobius.
• În cea de-a 22- a tranșă a universului cinematografic Marvel , Avengers: Endgame , care abordează problema călătoriilor în timp . După ce a înțeles că acesta din urmă se comportă ca o buclă, Tony Stark folosește banda Moebius ca o figură matematică pentru a rezolva problema explorării timpului.
• În cel de-al 21- lea episod din Sakura, Card Hunter, vedem Cartea „Lupa” reprezentată de o bandă Möbius care îi permite să modifice spațiul dorit într-un circuit închis și infinit.

Jocuri video

• „Mobius 1” este numele de cod ( numele de cod ) al pilotului controlat în jocul Ace Combat 4: Thunder Distant . Insigna sa personală este o panglică Möbius.
• „Mobius Ring” este o cursă a jocurilor F-Zero AX și F-Zero GX lansate în Arcade și pe Gamecube .
• „Labirintul Möbius” este una dintre cele opt locații ascunse din jocul de rol Light of Oblivion lansat pentru PlayStation și PC .
• „Möbius” era ceea ce mulți credeau că este numele mondial al Sonic în Europa și Statele Unite înainte ca jocul Sonic Adventure să fie lansat în 1999. A fost de fapt o eroare de traducere în timpul unui interviu cu Yuji Naka (co-creator al Sonic) care a vorbit tocmai a unui motiv al decorului în spirală, pe care l-a descris ca „panglică Möbius”. Eroarea a fost atât de bine preluată încât vom găsi numele lui Möbius care desemnează planeta în care locuiește Sonic în benzile desenate ale lui Archie.
• În Sonic Riders: Zero Gravity , cursa finală are forma unei benzi Möbius și poartă numele său englez, Mobius Strip.
• În STALKER: Clear Sky pe PC , eroul face aluzie la banda Möbius pentru a ilustra efectul unei „bule anormale” care îi aduce neobosit pe cei care intră înapoi la punctul lor de plecare.
• În StarCraft 2 , găsim „Fundația Möbius”, un grup misterios în căutarea artefactelor Protoss.
• În seria Legacy of Kain , Moëbius este păstrătorul timpului.
• În Mario Kart 8 pe Wii U , pista Mario Circuit are forma unei benzi Möbius, la fel ca „8” din sigla jocului.
• În Makoto Mobius, personajul principal folosește o bandă Möbius pentru a reveni în timp.

Jocuri de cărți de colecție

• În Magic: The Gathering, există o carte numită „Panglică de Boeziu” ( anagrama lui Moebius) care vă permite să refolosiți anumite vrăji din cimitir. Ilustrația sa reprezintă o panglică metalică pe o singură față.

Romane

• În 2010: Odyssey Two , aberația comportamentală a computerului HAL 9000 este denumită „buclă Hofstadter -Möbius”.
• În Hyperion de Dan Simmons , Cube Mobius conține energia produsă de erg-uri.
• În L'Anneau de Moebius , 2008, de Franck Thilliez , inelul este de fapt schița poveștii ... (Trebuie să-l citiți pentru a înțelege.)
• În Îngeri și demoni , de Dan Brown , la punctul 31.
• În seria Necroscop a lui Brian Lumley , eroul Harry Keogh, afișează frecvent Mobius pentru a deschide o ușă pentru a naviga spațiul-timp.
• În Trap on Zarkass , 1958, de Stéfan Wul, autorul bazează accesul la subspațiu prin trei benzi Möbius cuibărite împreună.
• În Cités de Mémoire , 2002, de Hervé Le Tellier , orașul Suibeom ( palindromul „Moebius”) pare să aibă structura unei benzi Möbius.

Sculpturi și grafică

• Max Bill a sculptat mai multe panglici Möbius, dintre care una este expusă în special la Middelheim Open Air Sculpture Museum , în parcul cu același nume din Anvers , Belgia. Puteți vedea, de asemenea, unul dintre inelele sale de granit Endless in the Centre Pompidou din Paris .
• Wim Delvoye , artist contemporan belgian, a expus la Muzeul Luvru o serie de crucifixuri metalice răsucite în apartamentele lui Napoleon al III-lea.
• Maurits Cornelis Escher , gravor și desenator olandez (1898-1972), a făcut numeroase studii asupra panglicii Möbius.
• Pentru aniversarea a 20 - a Warp Records înregistrare eticheta , o serie de imagini cu panglici Mobius a fost creat de Studio DA cu fotograful Dan Holdsworth. Unele dintre ele au fost folosite ca ilustrații pentru compilații .
• Alice Pilastre a creat o lucrare numită Mobius Gymnopedy , alcătuită dintr-o cutie muzicală în care panglica metalică care poartă partitura are forma unei panglici Mobius. Această casetă conține primele note ale primelor Gimnopedii ale lui Erik Satie . Când derulați banda, veți auzi aceste note, apoi aceleași cele cu un pas inversiune .
• Un imens inel Möbius este reprezentat sub forma unei sculpturi în Lille , în districtul Wazemmes . Această sculptură, creată de Marco Slinckaert, ocupă centrul unui sens giratoriu din fața CPAM . De asemenea, se numește șarpe prin marea sa asemănare. O altă sculptură se află la Universitatea din Rennes I , pe campusul Beaulieu .
• Keizo Ushio ciopleste panglici Möbius tăiate de-a lungul liniei lor centrale.
• Ellen Heck, artist gravor, folosește motivul panglicii Möbius în seria sa Fascinators  : portrete de tinere care poartă panglica Möbius, exprimând întrebări abstracte legate de feminitate.
• Designerul Jean Giraud , alias Mœbius, și-a luat pseudonimul din panglica menționată

La Lacan

În vocabularul lui Jacques Lacan  : „1962/63 - Angoasa - 01/09/63 - Ce face o imagine speculară distinctă de ceea ce reprezintă? este pentru că dreapta devine stânga și invers. - O suprafață unilaterală nu poate fi răsturnată. - Deci, o bandă Moebius, dacă întoarceți una asupra sa, va fi întotdeauna identică cu ea însăși. Aceasta este ceea ce numesc neavând nicio imagine în oglindă. "

Din punct de vedere matematic, afirmația anterioară a lui Lacan este eronată: am văzut în secțiunile anterioare că imaginea în oglindă a unei benzi Möbius corespunde unei inversări (înainte de lipire) a unei jumătăți de tură în cealaltă direcție și, prin urmare, nu este identic cu panglica inițială (mai general, dacă imaginea în oglindă a unei figuri poate fi suprapusă peste ea printr-o deplasare, este pentru că figura are un plan de simetrie) .

La Patrick Tort

În epistemologia lui Patrick Tort , metafora topologică a benzii Möbius ilustrează ceea ce el numește efectul reversiv al evoluției în Darwin  : selecția naturală, născută din lupta pentru existență, selectează instinctele sociale, a căror dezvoltare în „civilizație” este din ce în ce mai opusă. la lupta pentru existență și, prin urmare, la selecția naturală.

Imaginea benzii Möbius este utilizată pentru a explica operația reversivă. Compus dintr-o bandă (2 laturi) închisă după răsucire cu o jumătate de tură, are acum o singură latură și o singură margine. Dacă numim cele două fețe inițial opuse „natură” și „civilizație”, vedem că trecem, la jumătatea drumului, de la una la alta fără să sarim sau să ne rupem (nu ar putea exista în cadrul continuității „genealogice” care rămâne fundamentală aici). Continuismul darwinist în antropologie nu este simplu, ci reversiv. Mișcarea natură → cultură nu produce o ruptură, dar impune totuși dovezi tangibile ale unui „efect de ruptură”, deoarece am trecut treptat „la cealaltă parte”.

Note și referințe

1. (în) [video] Tadashi Tokieda, Geometry & Topology - Reading 01 Part 01/02 pe YouTube .
2. Inelul Möbius și reciclarea .
3. (în) „  Computer Graphic este încă considerată o nouă tehnologie în divertisment în China  ” , 8 martie 2006.
4. La Minute du geek difuzat pe canalul de televiziune Nolife din 20 mai 2009 (abonament necesar pentru vizionare online) .
5. http://www.drunkenboat.com/db8/oulipo/feature-oulipo/oulipo/texts/le_tellier/sighted_fr.html#Suibeom .
6. Alice Pilastre pe site-ul Kikk Festival 2013.
7. (în) [PDF] Buletinul informativ al Societății Internaționale a Artelor, Matematicii și Arhitecturii , septembrie 2006.

Anexe

Bibliografie

• (ro) Udo Hertrich-Jeromin , Introducere în geometria diferențială Möbius , CUP ,2003
• (ro) Jonathan D. Amith , The Möbius Strip: A Spatial History of Colonial Society din Guerrero, Mexic , Stanford University Press ,2005
• S. Wane , Africanity and Africanization of the West , Le Publieur,2012
• (ro) Chen Nanxian , Mobiüs inversion in Physics , World Scientific ,2010
• Frank Thilliez , Inelul lui Moebius , Pasajul ,2008

Articole similare

• Sticla Klein
• Scara Möbius
• Flexagon
• Lemniscate
• Roller coaster în inelul Möbius
• Orientare (matematică)
• Acoperire (matematică)
• Suprafața băiatului

linkuri externe

Matematică

• Ecuații și reprezentări (site-ul MathCurve)
• Reprezentarea ca suprafață

Pragmatic

• „Realizarea benzii, particularitățile și proprietățile tăieturilor” (pe arhiva Internet )

Muzică

• Animația canon cancrizans de către JS Bach pe o bandă Möbius , extras din Oferta muzicală