Icosaedru
| Icosaedru regulat | |
| |
| Tip | Solid platonic |
|---|---|
| Fețe | 20 de triunghiuri echilaterale |
| Margini | 30 |
| Vârfuri | 12 |
| Fețe / vârf | 5 |
| Caracteristică | 2 |
| Simbolul Schläfli | {3.5} |
| Simbolul Wythoff | 5 |
| Diagrama Coxeter-Dynkin |
|
| Dual | Dodecaedru regulat |
| Grup de simetrie | Eu h |
| Volum | |
| Zonă | |
| Unghi diedru | 138,19 ° |
| Proprietăți | Convex , regulat |
În geometrie , un icosaedru este un solid tridimensional , din familia poliedrelor , conținând exact douăzeci de fețe . Prefixul icosa- , de origine greacă , înseamnă „douăzeci”.
Există un icosaedru convex regulat . Se spune că un poliedru este regulat dacă toate fețele sale sunt identice cu același poligon regulat și dacă, de la fiecare vârf, începe același număr de muchii. Se spune că este convex dacă orice segment ale cărui capete sunt în interiorul poliedrului este complet în interiorul poliedrului. Există 5 poliedre atât regulate, cât și convexe: solide platonice .
Deoarece are trei vârfuri pe față și cinci fețe pe vârf, simbolul Schläfli al icosaedrului regulat este {3,5}.
Scheletul icosaedrului regulat - ansamblul vârfurilor sale legate de marginile sale - formează un grafic numit grafic icosaedru .
Grupul de rotații ale icosaedru, format prin rotațiile spațiului care părăsesc acest poliedru global invariant în timp ce permutării anumite fețe, cuprinde 60 de elemente și este izomorf la grupa alternante A 5 .
Un alt solid platonic are același grup de rotații ca și icosaedrul: dodecaedrul regulat . Se obține considerând solidul ale cărui vârfuri sunt centrele fețelor unui icosaedru. În schimb, obținem un icosaedru considerând solidul având pentru vârfuri centrele fețelor unui dodecaedru regulat. Spunem că icosaedrul și solidele platonice ale dodecaedrului sunt duale .
Geometria icosaedrului convex regulat
Modele ale unui icosaedru
Un icosaedru este construit folosind 20 de triunghiuri echilaterale de aceeași dimensiune. Începem prin asamblarea a 5 dintre triunghiuri de marginile lor în așa fel încât să formeze un castron cu un vârf în partea de jos. Astfel, baza solidului este un vârf împărțit de cele 5 triunghiuri, iar marginea este compusă din 5 segmente, toate de aceeași lungime, formând un pentagon regulat. Pe fiecare dintre cele 5 segmente care formează suprafața bolului, lipim un nou triunghi, astfel încât partea superioară a fiecărui triunghi al bolului să fie și partea inferioară a unuia dintre cele 5 triunghiuri adăugate. Apoi îndreptați cele 5 triunghiuri superioare astfel încât fețele lor să fie verticale. Se obține apoi un castron mai mare, compus din 10 triunghiuri, a cărui parte superioară este formată din 5 dinți .
Construim o a doua formă identică cu prima. Au fost apoi folosiți toți cei 20 de triunghiuri. A doua formă se potrivește exact în prima, formând un poliedru regulat. Este prezentat în figura 2, bolul inferior este albastru. Observăm capacul inferior, apoi cei 5 dinți, dintre care 3 sunt orientați spre un observator și 2 în spate. Vasul superior, în roșu în figură, are aceeași geometrie. Pentru a le potrivi, așezați pur și simplu capacul în partea de sus și 2 dinți în fața observatorului.
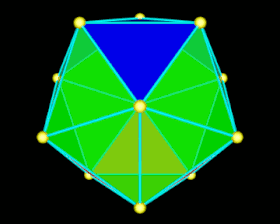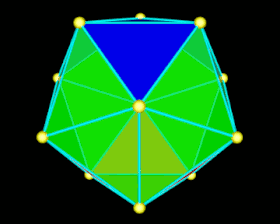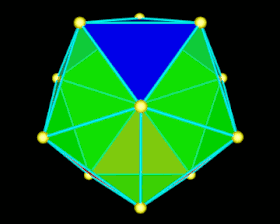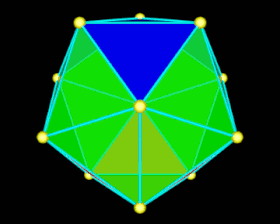
Încă putem construi icosaedrul folosind modelul ilustrat în figura 1. Icosahedronul se obține prin lipirea laturii libere a triunghiului galben în partea stângă sus pe partea liberă a triunghiului portocaliu, în partea dreaptă jos. Cele 5 triunghiuri roșii, conectate la triunghiurile portocalii, sunt apoi abordate astfel încât vârfurile lor libere să se contopească într-un singur punct. Aceeași operație, efectuată pe cele 5 triunghiuri roșii, conectate la triunghiurile galbene, completează construcția icosaedrului. Modelul prezentat aici este un exemplu, există multe altele. Sunt 43.380.
Proprietăți
Un icosaedru are 20 de fețe. Are 12 vârfuri, 1 în partea de jos, 5 la baza inferioară a dinților descrise în prima construcție și tot atâtea pentru bolul superior. Are 30 de muchii: fiecare dintre cele 12 vârfuri este comun la 5 muchii, sau 60, dar din moment ce o margine conține 2 vârfuri, trebuie să împărțiți 60 la 2 pentru a obține rezultatul corect.
Vârfuri, muchii și fețe - Un icosaedru convex obișnuit conține 12 vârfuri, 30 de margini și 20 de fețe. Unghiul diedru (unghiul format din două fețe adiacente) este de 138,19 °.
Cele mai mari segmente incluse în poliedru se termină cu două vârfuri ale poliedrului. Există 6 dintre ele și intersecția acestor 6 segmente este un punct, numit centrul poliedrului . Acest punct este, de asemenea, centrul de greutate al solidului. Există 10 segmente de capăt în două puncte ale suprafeței poliedrului, care trec prin centru și cu lungime minimă. Capetele sunt centrele a două fețe opuse, sunt paralele între ele. Aceste observații geometrice fac posibilă calificarea sferei circumscrise și a celei inscripționate a solidului. Sfera circumscrisă este cea a cea mai mică rază, interiorul care conține interiorul poliedrului. Această definiție o generalizează pe cea a unui cerc circumscris . De asemenea, putem vorbi despre o sferă inscripționată pentru a indica cea a razei celei mai mari al cărei interior este inclus în interiorul solidului, generalizând astfel definiția cercului inscris .
Sferele circumscrise și inscripționate - Sfera circumscrisă a icosaedrului are același centru ca și solidul și conține toate vârfurile poliedrului. Sfera înscrisă în icosaedru are același centru și conține centrul fiecărei fețe a acestui poliedru.
O analiză rapidă ar putea sugera că există un cerc care conține 6 vârfuri ale poliedrului. Nu este cazul: un cerc conține maximum 5 vârfuri. Această eroare este, de exemplu, făcută de Albrecht Dürer , pictor al XVI - lea secol . Pe de altă parte, Dürer nu face o greșeală atunci când afirmă că:
Cub circumscris - Cel mai mic cub care conține icosaedrul are același centru ca și solidul, suprafața acestuia conține toate vârfurile poliedrului.
Această proprietate este ilustrată în Figura 4. Fiecare dintre fețele cubului conține două vârfuri și o margine a poliedrului. Cubul conține 6 fețe, deci cele 12 vârfuri.
Structura acestui poliedru este regulată. Marginile au toate aceeași lungime, două margini ale aceleiași fețe și având un vârf comun formează întotdeauna același unghi, egal cu 60 de grade sau chiar cu π / 3, dacă măsura unghiului este radianul . Numărul de muchii care împart același vârf este o constantă care nu depinde de vârful ales. Vorbim despre un poliedru regulat . Un segment cu cele două capete ale sale în interiorul solidului este complet în interiorul solidului; spunem că icosaedrul este convex . Un alt mod de a-l privi este să observați că o bandă de cauciuc care înconjoară solidul îl atinge în fiecare punct. Aceste două moduri de a vedea sunt echivalente. Poliedrele regulate nu sunt întotdeauna convexe (vezi „ Kepler-Poinsot solid ”). Poliedrele convexe regulate se numesc solide platonice .
Solid platonic - Există un icosaedru convex regulat.
Simetrie
O izometrie afină părăsește un poliedru care este global invariant atunci când imaginea acestui solid prin izometrie ocupă exact aceeași poziție ca și cea inițială. Vârfurile, marginile și fețele pot fi schimbate, dar poziția generală este neschimbată. Determinantul unei izometrie este egală cu ± 1 . Toate izometriile unui poliedru își fixează centrul. Cele ale determinantului 1 (sau deplasărilor ), numite „simetriile proprii” ale poliedrului, sunt deci rotații și - prin multiplicativitatea determinantului - cele ale determinantului –1 , numite „simetriile necorespunzătoare”, sunt compușii unuia dintre ' între ele (dacă există) prin aceste rotații.
Rotații ale icosaedrului - Există 60 de rotații care lasă icosaedrul (convex regulat) la nivel global invariabil: rotația unghiului zero, 15 rotații la jumătate, 20 rotații la o treime și 24 rotații la jumătate și 24 rotații la jumătate un unghi multiplu de o cincime de tura.
Axa unei astfel de rotații trece în mod necesar prin centrul poliedrului și trece fie printr-un vârf, fie prin mijlocul unei margini, fie prin mijlocul unei fețe.
Să studiem mai întâi rotațiile (de unghi diferit de zero) a căror axă conține centrul unei muchii. O astfel de rotație trebuie să schimbe cele două vârfuri ale muchiei respective, deci este o întoarcere în U. În Figura 5, am grupat vârfurile icosaedrului în planuri perpendiculare pe axa de rotație (în albastru), pentru a evidenția cinci seturi. Cele două extreme (în albastru) sunt compuse din două puncte care formează marginile care delimitează solidul și care traversează în mijlocul lor axa studiată. Găsim apoi două seturi de două puncte (în roșu) care se află pe două linii perpendiculare atât pe segmentele albastre, cât și pe axa de rotație. În cele din urmă, în mijlocul poliedrului, există patru puncte (în verde) care formează un dreptunghi . Aceste cinci figuri sunt invariante printr-o rotație de o jumătate de tură. Deducem existența unei rotații de o jumătate de tură pentru fiecare pereche de margini opuse. Deoarece există 30 de muchii, există 15 rotații la jumătate de tură.
Rețineți în treacăt că putem grupa 3 la 3 aceste 15 jumătăți de rotație, pe grupuri de trei rotații de axe două câte două perpendiculare, și care, prin urmare, fac naveta .
Figura 6 ilustrează cazul unei rotații (cu unghi diferit de zero) a cărei axă trece prin centrul a două fețe opuse. O astfel de rotație trebuie să permute cele trei vârfuri ale fiecăreia dintre aceste două fețe, deci este o treime dintr-o rotație. Aceeași tehnică ca cea folosită anterior grupează de această dată vârfurile în patru seturi. Prin construcție, cele două seturi extreme sunt fețe. Acestea sunt triunghiuri echilaterale de aceeași dimensiune și rotite la jumătate față de celălalt. Cele două mulțimi centrale, în violet în figură, sunt, de asemenea, triunghiuri mai mari, echilaterale. O rotație de o jumătate de tură este necesară pentru a face să coincidă două triunghiuri situate unul lângă celălalt.
Există 2 rotații de o treime de rotație pe pereche de fețe. Solidul conține 20 de fețe; deducem că există 20 de rotații de această natură.
Figura 7 ilustrează cazul unei rotații a cărei axă trece prin două vârfuri opuse. O astfel de rotație trebuie să permită cele cinci muchii care trec prin fiecare dintre aceste două vârfuri, deci este un multiplu al unei cincimi de ture. Vârfurile sunt încă grupate în 4 seturi. Cele două extreme sunt compuse dintr-un singur punct, cele două seturi cele mai apropiate de centru formând fiecare un pentagon regulat. Au aceeași dimensiune și sunt încă compensate cu o jumătate de tură. Există 4 rotații ale axelor care trec prin două vârfuri, lăsând solidul global invariant, dacă una neglijează rotația unghiului zero. Există 12 vârfuri și 6 axe care conțin două vârfuri opuse sau 24 de rotații de această natură.
Simetriile necorespunzătoare ale icosaedrului - Există 60 de simetrii necorespunzătoare care părăsesc icosaedrul (convex regulat) global invariante: simetrie centrală față de centrul solidului, 15 reflecții (simetrii ortogonale în raport cu planurile), 20 roto-inversiuni d treimea unui viraj și 24 roto-inversiuni ale unui unghi multiplu al unei cincimi de viraj
Într-adevăr, diferitele ilustrații precedente arată toate că această simetrie centrală lasă acest solid invariant la nivel global și orice rotire-inversiune a unghiului α (produsul unei rotații a unghiului α printr-o simetrie a centrului un punct al axei) este un anti - rotația unghiului α + π (produs al rotației unghiului α + π printr-o reflecție dintr-un plan perpendicular pe axă), deci o reflecție dacă α = π.
Figuri remarcabile ale icosaedrului
Simetriile de ordinul 3 și 5 introduc figurile geometrice plane asociate cu aceste simetrii.
O simetrie plană de ordinul 3 are pentru grupul de simetrie triunghiul echilateral (cf. „ Rețea (geometrie) ”). Este firesc să-i găsești urme în icosaedru. Este posibil să construim astfel de triunghiuri cu vârfurile diferite ale solidului. Fiecare axă care trece prin centrul a două fețe opuse traversează în centrele lor 4 triunghiuri echilaterale. Două dintre aceste triunghiuri sunt fețe. Celelalte două, prezentate în violet în Figura 6, au o latură în proporția rațiunii extreme și medii în raport cu o margine a poliedrului. Aceasta înseamnă că latura unui dreptunghi violet împărțit la lungimea unei margini este egală cu raportul auriu.
Pentru fiecare pereche de fețe, există 2 triunghiuri echilaterale mici și 2 mari, ceea ce face un total de 12 triunghiuri echilaterale mici și tot atâtea mari.
Prezența numărului de aur nu este deloc surprinzătoare, ea intervine în exprimarea unei rotații de ordinul 5 și, în consecință, în raporturile de dimensiune ale unui pentagon. Paralel cu fiecare axă care trece prin două vârfuri opuse, există doi pentagoni al căror plan este ortogonal cu axa. Fiecare vârf al pentagonului este, de asemenea, un vârf de două triunghiuri aurii cu geometrii diferite. Se spune că un triunghi este auriu când este isoscel, iar latura mare și cea mică sunt proporționale cu rațiunea extremă și medie. Există două tipuri diferite, cele cu două laturi lungi, în gri în Figura 8, și cele cu două laturi scurte, în galben. Fiecare vârf al unui pentagon este vârful adiacent la două laturi egale ale unui triunghi auriu de fiecare tip. Figura conține 2 pentagone sau 10 vârfuri și 20 de triunghiuri aurii. Există 6 axe diferite care trec prin două vârfuri opuse sau 120 de triunghiuri aurii.
Există, de asemenea , dreptunghiuri aurii , adică dreptunghiuri a căror lungime și lățime au un raport egal cu numărul auriu. Există exact 1 per latură a pentagonului, a doua latură este apoi localizată pe celălalt pentagon. Un exemplu este prezentat în verde în Figura 8. Deoarece există 5 perechi de astfel de margini pentru fiecare pereche de pentagone, există 30 de dreptunghiuri aurii.
Poliedru dual
Folosind un poliedru regulat, este posibil să se construiască unul nou, cu vârfurile centrelor fețelor solidului inițial. Dualul unui solid platonic este încă un solid platonic.
În cazul unui icosaedru, dualul are 20 de vârfuri și fiecare față este un pentagon regulat, deoarece fiecare vârf este împărțit de 5 margini. Poliedrul obținut este un dodecaedru convex regulat , un solid compus din 12 fețe pentagonale. Dimpotrivă, dualul unui dodecaedru, un solid platonic, este un poliedru regulat convex cu 12 vârfuri. Deoarece fiecare vârf al dodecaedrului este împărțit de 3 margini, fețele dualului său sunt triunghiuri echilaterale. Recunoaștem icosaedrul. Această proprietate este generală pentru poliedre, dualul dualului unui poliedru este o omotitate a solidului inițial.
O simetrie care lasă icosaedrul global invariant lasă, de asemenea, toate punctele medii ale fețelor sale invariante. Deducem că orice simetrie a icosaedrului este, de asemenea, o simetrie a dodecaedrului. În schimb, același raționament arată că orice simetrie a dodecaedrului este, de asemenea, o simetrie a icosaedrului. Cele două seturi de izometrii asociate celor două poliedre duale sunt aceleași. Aici, termenul de simetrie este folosit în sensul izometriei.
Cantități caracteristice
Tabelul următor prezintă diferitele dimensiuni caracteristice ale icosaedrului convex regulat:
| Dimensiunile unui icosaedru a cărui lungime a muchiei este a | ||
|---|---|---|
| Unghi diedru | ||
| Raza sferei circumscrise | ||
| Raza sferei inscripționate | ||
| Marginea cubului circumscris | ||
| Înălțimea icosaedrului (distanța dintre două fețe opuse) |
||
| Volum | ||
| Fracțiunea sferei circumscrise ocupată | ||
| Zonă | ||
| Cocient isoperimetric | ||
Unghiul diedru este unghiul dintre două planuri conținând fiecare o față a icosaedrului, cele două fețe având o margine comună.
Fascinația icosaedrului
- În Timeu , Platon , după ce a descris cele cinci poliedre regulate convexe, atribuie fiecăruia dintre primii patru un element al universului. Cu icosaedrul, el asociază apa care, după el, este cea mai puțin mobilă formă, după cub, adică cea care trebuie să aibă cele mai multe fețe și vârfuri. El observă astfel că este nevoie de două corpuri și jumătate de aer (octaedru) pentru a construi un element de apă (icosaedru) și că un element de apă poate fi distrus de foc (tetraedru) pentru a forma 5 elemente de foc. Platon clasifică printre elementele apei, printre altele, aurul, diamantul și alama.
- În unele jocuri de rol , zarurile la 20 de fețe (prescurtat D20 ) sunt folosite pentru a determina succesul sau eșecul unei acțiuni. Această matriță este un icosaedru.
- În biologia moleculară , mulți viruși , cum ar fi virusul herpesului , au forma unui icosaedru. Cele capsidele sunt formate din subunități proteice identice repetate, iar forma unui icosaedru este forma cea mai potrivită pentru a asambla aceste subunități, deoarece permite un spațiu maxim pentru genomului . Într-adevăr, printre solidele platonice de volum dat, icosaedrul este cel a cărui sferă inscripționată este cea mai mare.
- Prin înlocuirea fiecărei margini a icosaedrului cu o rezistență de 1 ohm , măsurarea rezistenței între două colțuri opuse dă 0,5 ohm, iar între două colțuri adiacente 11/30 ohmi.
- Proeminenței Fuller (sau hartă Dymaxion, creat de Richard Buckminster Fuller ) este o proiecție gnomonic a unui icosahedron.
- Alexandre Grothendieck , așa cum spune el în biografia sa, a fost întotdeauna fascinat de icosaedru. La sfârșitul carierei sale, la Universitatea din Montpellier , el le-a oferit studenților săi un examen de reflecție în care trebuia să construiască un icosaedru din hârtie și le-a dat tuturor note excelente, ceea ce a provocat un scandal printre colegii săi.
- Un icosaedru a fost găsit într-un mormânt roman din Aléria, în Corsica. Poate fi văzut la muzeul Aléria.
Structura matematică a unui icosaedru, solid platonic
Construcție pe coordonate
Prima parte a acestui articol prezintă mai multe rezultate, dar nici o dovadă. Însăși existența unui icosaedru convex regulat nu este demonstrată. O metodă simplă constă în determinarea punctelor, candidații la vârfurile unui poliedru regulat convex. Abordarea utilizată aici constă în găsirea unui set de puncte E având 4 proprietăți care sunt verificate dacă aceste puncte sunt vârfurile icosaedrului:
- mulțimea E are 12 vârfuri;
- există o sferă care conține toate punctele lui E ;
- poliedrul P , înveliș convex al lui E , are fețe toate formând triunghiuri echilaterale;
- dacă am ales inteligent reper , înmulțiți coordonat orice un summit cu un -1 punct E da încă un punct E .
Ultima proprietate este o consecință a stabilității icosaedrului prin trei rotații de jumătate de tură și axe perpendiculare două câte două. Pentru calcule simple, este o idee bună să setați lungimea unei muchii la 2 și să o poziționați pe cea mai îndepărtată spre dreapta, paralel cu axa y. Obținem următoarele coordonate:
Aici φ denotă numărul de aur , egal cu (1 + √ 5 ) / 2. Odată stabilite coordonatele, avem o dovadă a existenței unui icosaedru convex regulat cu 12 vârfuri. Putem arăta într-adevăr că P este un poliedru regulat cu 12 vârfuri. Este suficient să se verifice că, pentru orice vârf, există exact 5 muchii care conțin acest vârf, că au aceleași lungimi și că aceste 5 muchii definesc într-adevăr 5 triunghiuri echilaterale.
Aceste coordonate permit, de asemenea, calcularea constantelor caracteristice ale icosaedrului, descrise în paragraful anterior.
Detalii de calculÎncercăm să construim mulțimea E , cu centrul vectorului zero și ale cărui margini sunt de lungime 2. Alegem ca bază ortonormală ( e 1 , e 2 , e 3 ), definită în caseta derulantă care precede a treia propoziție. Fie S 1 un punct al lui E astfel încât prima sa coordonată să fie cea mai mare posibilă și să fie ( a , b , c ) coordonatele lui S 1 .
- Chiar dacă înseamnă permutarea e 2 și e 3 , coordonatele lui S 1 sunt ( a , 1, 0) și există alte trei puncte S 2 , S 3 și S 4 ale E , cu coordonate ( a , –1, 0 ), (- a , 1, 0) și (- a , –1, 0):
Este cunoscut faptul că este posibil să se multiplice fiecare coordonată a unui punct E de -1 , fără a părăsi set, deducem că cele patru puncte ( a , ± b , ± c ) sunt în E . Deoarece aceste puncte sunt cele mai în dreapta lui E , ele sunt situate pe aceeași față. Nici o față nu conține 4 puncte, deducem că fie b, fie c este zero. Chiar dacă înseamnă permutarea e 2 și e 3 , putem alege c nul. Marginea de la capătul axei de rotație a grupului de simetrie, direcționată de e 1 are pentru capătul S 1 al coordonatelor ( a , b , 0) și S 2 al coordonatelor ( a , - b , 0). O muchie are o lungime de 2, ceea ce arată că b este egal cu 1.
Deoarece este posibil să se înmulțească cu –1 orice coordonată a unui vârf pentru a obține coordonatele unui nou vârf, cele două puncte (- a , ± 1, 0) sunt, de asemenea, vârfuri.
- Cele 4 puncte suplimentare S 5 până la S 8 cu coordonatele respective (1, 0, a ), (–1, 0, a ), (1, 0, - a ) și (–1, 0, - a ) sunt în E :
Același raționament ca mai sus permutând baza ( e 1 , e 2 , e 3 ) în ( e 3 , e 1 , e 2 ) produce patru puncte S 5 , S 6 , S 7 și S 8 din E , de coordonate ( f , 1, 0), ( f , -1, 0), (- f , 1, 0) și (- f , –1, 0) în noua bază și în coordonatele (1, 0, f ), (- 1, 0, f ), (1, 0, - f ) și (–1, 0, f ) în baza inițială.
Pătratul normei lui S 5 este egal cu 1 + f 2 . Este încă egală cu pătratul standardului S 1 , adică 1 + un 2 , pentru că există o sferă centrală a vectorului de zero, care conține toate punctele de E . Deoarece a și f sunt alese pozitive, a este egală cu f . Aceasta completează dovada propunerii.
- Valoarea lui a este egală cu raportul auriu:
Distanța care separă S 1 de S 5 este egală cu 2, ceea ce dă următoarea ecuație:
Ecuația precedentă admite o soluție pozitivă unică. Prin definiție, această valoare este egală cu raportul auriu.
- Cele 4 puncte S 9 până la S 12 cu coordonatele respective (0, φ, 1), (0, φ, –1), (0, –φ, 1), (0, –φ, –1) sunt ultimele 4 punctele E :
Același raționament ca mai sus prin interschimbarea bazei ( e 1 , e 2 , e 3 ) în ( e 2 , e 3 , e 1 ) produce patru puncte S 9 , S 10 , S 11 și S 12 din S . de coordonate ( φ , 1, 0), ( φ , -1, 0), (- φ , 1, 0) și (- φ , –1, 0) în noua bază și de coordonate (0, φ , 1 ), (0, φ , -1), (0, - φ , -1) și (0, φ , -1) în baza inițială.
Calculul constantelor caracteristice ale icosaedrului.Pentru a fi riguros, este necesar să arătăm că corpul convex al punctelor lui E formează într-adevăr un poliedru regulat. Calculul direct este puțin obositor, următorul paragraf oferă o dovadă alternativă. Analiza reprezentărilor unui grup de 60 de elemente arată existența unui solid platonic cu 12 vârfuri și care conține triunghiuri echilaterale ca fețe și că cele 12 vârfuri sunt situate pe o sferă. De asemenea, arată existența a 3 rotații ale unei jumătăți de rotație și a axelor ortogonale două câte două. Deoarece cele 12 puncte ale lui E corespund soluției unice, cu excepția unei rotații, verificând aceste proprietăți dacă lungimea unei muchii este egală cu 2, învelișul său convex este în mod necesar un icosaedru regulat.
Calculele coordonatelor vârfurilor arată, prin omotitatea raportului a / 2, dacă a este un real strict pozitiv, că coordonatele unui icosaedru convex regulat sunt, într-un cadru bine ales:
- Raza sferei circumscrise este egală cu r ext , cu:
Punctele celor mai mari norme ale icosaedrului sunt vârfurile, raza r ext este egală cu norma unui vârf și:
- Raza sferei inscripționate este egală cu r int , cu:
Punctele celor mai mici norme ale suprafeței icosaedrului sunt punctele medii ale fețelor. Punctul M cu coordonatele date de următoarele calcule este punctul de mijloc al unei fețe:
Un calcul al normei lui M face posibilă finalizarea determinării:
- Marginea cubului circumscris este egală cu a φ:
Marginea cubului circumscris are o lungime egală cu distanța dintre două centre ale muchiilor opuse ale icosaedrului. Punctul coordonatelor ( a φ / 2, 0, 0) este centrul unei muchii. Centrul muchiei opuse are pentru coordonate (- a φ / 2, 0, 0), ceea ce permite deducerea rezultatului.
- Zona de poliedrului este egal cu 5 √ 3 a 2 :
O față este un triunghi echilateral cu latura a . Înălțimea sa este dată prin aplicarea teorema lui Pitagora , există o √ cu 3 /2. Suprafața sa este produsul de jumătate din lungimea de o parte de înălțime, există un 2 √ cu 3 / , 4. Suprafața poliedrului este compusă din 20 de fețe, ceea ce face posibilă găsirea rezultatului.
- Volumul poliedrului este egal cu V , cu:
Icosaedrul este împărțit în 20 de conuri cu vârful centrul solidului și o față de bază a zonei S f . Deducem formula, dacă d reprezintă distanța dintre centrul solidului și cel al unei fețe:
- Un icosaedru ocupă o fracțiune V / V s din volumul sferei circumscrise, cu:
Raza sferei circumscrise este egală cu r ext , o valoare deja calculată. Deducem volumul V s al sferei:
Cunoașterea volumului icosaedrului vă permite să finalizați calculul:
- Cocient isoperimetric:
Această întrebare este tratată în articolul Isoperimetrie .
Grup de simetrie
În drept compoziție izometrii de spațiu euclidian de dimensiune 3 oferă toate aceste aplicații o structură de grup . Izometriile care părăsesc icosaedrul la nivel global formează un subgrup , de ordinul 120: grupul de simetrie al icosahedronului.
Teorema - Grupul de simetrie al icosedronului este izomorf cu produsul direct al grupului alternativ A 5 de grupul ciclic de ordinul 2.
Într-adevăr :
- articolul „ grup alternative “ arată că subgrupul rotațiile icosaedru este izomorf la grupa alternante A 5 (grupul de chiar permutări ale unui set de 5 elemente). Această dovadă asigură în treacăt existența unui solid platonic cu 12 vârfuri, 30 de muchii și 20 de fețe care sunt triunghiuri echilaterale (într-un anumit sens, există o singură modalitate de a reprezenta grupul A 5 ca un set 60 de rotații ale unui 3- spațiul euclidian dimensional);
- simetria centrală față de centrul poliedrului navetează la aceste 60 de rotații.
Aplicații
-
Icosahedral D20 utilizat în mod obișnuit în jocurile de rol de masă .
-
Proiecția Fuller în animație.
- La fel ca alte solide platonice, icosahedrele sunt adesea folosite în jocurile de rol de masă pentru a produce zaruri cu 20 de fețe, denumite în mod obișnuit ca d20.
- În domeniul proiecțiilor hărții , icosaedrul poate fi folosit pentru proiecția lui Fuller .
Note și referințe
- (în) F. Buekenhout și domnul Parker, " Numărul de rețea al politopilor conveși obișnuiți în dimensiunea ⩽ 4 " , Disc. Matematica. , vol. 186,1998, p. 69-94 ( DOI 10.1016 / S0012-365X (97) 00225-2 ).
- Albrecht Dürer , Geometrie , prezentare și traducere de Jeanne Peiffer, Seuil, Paris, 1995 ( ISBN 2020124270 ) , p. 31 .
- (în) Peter R. Cromwell, Polyhedra , Cambridge University Press, 1997 ( ISBN 0521664055 ) , pp. 53 .
- O analiză grafică este propusă de R. Ferréol, „ Icosaèdre ” .
- (în) Eric W. Weisstein , „ Icosahedron ” pe MathWorld .
- Timeu , 55-56.
- Timeu , 59b.
- Jean-Pierre Lavergne, „ Alexander Grothendieck, matematician rebel ” ,noiembrie 2014, (§ „Un juriu cu Grothendieck”).
- Aceste calcule pot fi găsite, de exemplu în Buekenhout și Parker 1998 .
- Un tabel de caractere (en) al acestui grup este furnizat în (en) JS Lomont, Applications of Finite Groups , Academic Press ,2014( 1 st ed. 1959) ( linia citit ) , p. 82.
Vezi și tu
Bibliografie
(ro) MJ Wenninger, Dual Models , Cambridge University Press, 2003 ( ISBN 0521543258 )
Articole similare
linkuri externe
- J. Drabbe și C. Randour-Gabriel, Un poliedru simbol al apei
- Icosaèdre pe recreomath.qc.ca
- Icosaèdre pe site-ul Universității Louis Pasteur din Strasbourg
- [video] Jolies Maths, Scheletul icosaedrului ... pe YouTube . Planurile „structurii interne” a icosaedrului (din 3 dreptunghiuri aurii).























