Tensor (matematică)
Cele Tensorii sunt obiecte matematice din algebra multiliniare de generalizare a scalar și vectorul . Acestea se găsesc în special în analiza vectorială și în geometria diferențială folosită frecvent în câmpurile tensoriale . Ele sunt, de asemenea, utilizate în mecanica mediilor continue.
Acest articol este dedicat numai tensorilor din spațiile vectoriale cu dimensiuni finite , deși există generalizări în dimensiune infinită și chiar pentru moduli .
Principiu general
Principiul este de a generaliza noțiunile de scalari și vectori în dimensiune finită. Tensorii de un anumit tip sunt ei înșiși membri ai unui spațiu vectorial:
- au un adaos și un produs de scalari ;
- acestea sunt independente de o alegere de bază, dar pot fi reprezentate prin tabele cu mai multe intrări pentru o anumită alegere de bază.
I se adaugă două operații: un produs, cunoscut sub numele de tensor , care permite multiplicarea a doi tensori (posibil cu naturi distincte), precum și o aplicație liniară care reduce dimensiunea lor, numită contracție .
După cum s-a menționat mai sus, scalarii și vectorii constituie exemple simple de tensori. Într-o bază dată, un vector (tensorul de ordinul 1) poate fi reprezentat de datele unui n -tuple de coordonate. N x n matricilor - care pot reprezenta endomorphisms , bivectors sau chiar forme biliniare în funcție de caz - formează o extensie a n -uples similar cu extensia reprezentată de n -uples în raport cu scalari. Obiectele care pot fi descrise prin matrici constituie, prin urmare, primele tipuri de tensori non-triviali, numiți tensori de ordinul 2. Prin prelungirea reflexiei ne putem imagina, încă informal, matrici cubice n × n × n , corespunzătoare tensorilor de „ordin 3 și așa mai departe.
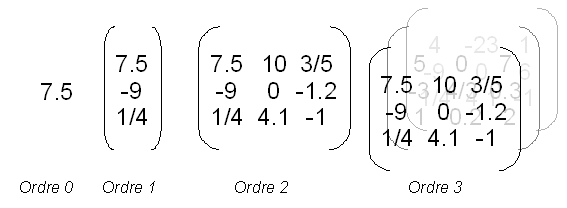
Cele două operații clasice ale manipulării tensoarelor pot fi ilustrate intuitiv prin anumite operații matriciale. De fapt, se știe că prin înmulțirea unei matrice de coloane cu o matrice de rânduri (adică două n- tuple) obținem o matrice pătrată (sau dreptunghiulară dacă operanzii nu au aceeași dimensiune). Prin urmare, există transformări care permit creșterea ordinii tensoarelor. Această idee este baza produsului tensor.
Dimpotrivă, produsul unei matrice de rând cu o matrice de coloană se reduce la un scalar. Aici vedem că apare ideea contracției.
Produs tensor al spațiilor vectoriale cu dimensiuni finite
Este practic, înainte de a studia produsul tensorial al vectorilor și de a da un sens mai precis termenului tensor, să se ia în considerare spațiile vectoriale care intervin în definirea acestuia. Rețineți că același simbol, și anume , este folosit pentru a construi atât tensorii, cât și spațiile la care aparțin.
⊗{\ displaystyle \ otimes}
Se va nota ulterior spațiul vectorial al aplicațiilor k- linéaires către in (adică liniar în raport cu fiecare dintre variabilele lor k ).
Lk(E1×⋯×Ek,F){\ displaystyle {\ mathcal {L}} _ {k} (E_ {1} \ times \ cdots \ times E_ {k}, F)} E1×⋯×Ek{\ displaystyle E_ {1} \ times \ cdots \ times E_ {k}}
E1×⋯×Ek{\ displaystyle E_ {1} \ times \ cdots \ times E_ {k}} F{\ displaystyle F}
F{\ displaystyle F}
Definiții
Fie și să fie două spații vectoriale cu dimensiuni finite peste un câmp comutativ (în practică este adesea o chestiune sau sunt posibile și alte câmpuri). Notăm dualul a . Produsul tensor al par - notat , sau dacă nu există nicio ambiguitate despre câmp - este un caz special al unui produs tensor al modulelor . O definiție mai simplă poate fi aici pentru a o defini ca spațiul vectorial al formelor biliniare pe perechea de spații vectoriale .
E{\ displaystyle E} F{\ displaystyle F}
F{\ displaystyle F} K{\ displaystyle \ mathbb {K}}
K{\ displaystyle \ mathbb {K}} R{\ displaystyle \ mathbb {R}}
R{\ displaystyle \ mathbb {R}} VS{\ displaystyle \ mathbb {C}}
VS{\ displaystyle \ mathbb {C}} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}} E{\ displaystyle E}
E{\ displaystyle E} E{\ displaystyle E}
E{\ displaystyle E} F{\ displaystyle F}
F{\ displaystyle F} E⊗KF{\ displaystyle E \ otimes _ {\ mathbb {K}} F}
E⊗KF{\ displaystyle E \ otimes _ {\ mathbb {K}} F} E⊗F{\ displaystyle E \ otimes F}
E⊗F{\ displaystyle E \ otimes F} (E∗,F∗){\ displaystyle (E ^ {*}, F ^ {*})}
(E∗,F∗){\ displaystyle (E ^ {*}, F ^ {*})}
E⊗F=L2(E∗×F∗,K){\ displaystyle E \ otimes F = {\ mathcal {L}} _ {2} (E ^ {*} \ times F ^ {*}, \ mathbb {K})}
De asemenea, se subliniază că, în dimensiunea finită, se asimilează fără probleme bidualului său . Prin urmare, avem același lucru:
E{\ displaystyle E} E∗∗{\ displaystyle E ^ {**}}
E∗∗{\ displaystyle E ^ {**}}
E∗⊗F∗=L2(E×F,K){\ displaystyle E ^ {*} \ otimes F ^ {*} = {\ mathcal {L}} _ {2} (E \ times F, \ mathbb {K})} E⊗F∗=L2(E∗×F,K){\ displaystyle E \ otimes F ^ {*} = {\ mathcal {L}} _ {2} (E ^ {*} \ times F, \ mathbb {K})}
E⊗F∗=L2(E∗×F,K){\ displaystyle E \ otimes F ^ {*} = {\ mathcal {L}} _ {2} (E ^ {*} \ times F, \ mathbb {K})} E∗⊗F=L2(E×F∗,K){\ displaystyle E ^ {*} \ otimes F = {\ mathcal {L}} _ {2} (E \ times F ^ {*}, \ mathbb {K})}
E∗⊗F=L2(E×F∗,K){\ displaystyle E ^ {*} \ otimes F = {\ mathcal {L}} _ {2} (E \ times F ^ {*}, \ mathbb {K})}
În teoria categoriilor , spațiile vectoriale (de dimensiune finită, dar putem generaliza la orice dimensiune) formează un exemplu standard de categorie monoidală pentru produsul tensorial astfel definit.
K{\ displaystyle \ mathbb {K}}
Proprietăți
Asociativitate
Spații vectoriale , și sunt canonicește izomorfe . Această proprietate face posibilă considerarea produsului tensorial ca asociativ și asimilarea produsului k spații de dimensiuni finite la spațiul formelor k- liniare pe spații duale. Prin urmare, parantezele nu sunt necesare:
(E⊗F)⊗G{\ displaystyle (E \ otimes F) \ otimes G} E⊗(F⊗G){\ displaystyle E \ otimes (F \ otimes G)}
E⊗(F⊗G){\ displaystyle E \ otimes (F \ otimes G)} L3(E∗×F∗×G∗,K){\ displaystyle {\ mathcal {L}} _ {3} (E ^ {*} \ times F ^ {*} \ times G ^ {*}, \ mathbb {K})}
L3(E∗×F∗×G∗,K){\ displaystyle {\ mathcal {L}} _ {3} (E ^ {*} \ times F ^ {*} \ times G ^ {*}, \ mathbb {K})}
(E⊗F)⊗G{\ displaystyle (E \ otimes F) \ otimes G} =E⊗(F⊗G){\ displaystyle = E \ otimes (F \ otimes G)}
=E⊗(F⊗G){\ displaystyle = E \ otimes (F \ otimes G)} =L3(E∗×F∗×G∗,K){\ displaystyle = {\ mathcal {L}} _ {3} (E ^ {*} \ times F ^ {*} \ times G ^ {*}, \ mathbb {K})}
=L3(E∗×F∗×G∗,K){\ displaystyle = {\ mathcal {L}} _ {3} (E ^ {*} \ times F ^ {*} \ times G ^ {*}, \ mathbb {K})} E1⊗⋯⊗Ek{\ displaystyle E_ {1} \ otimes \ cdots \ otimes E_ {k}}
E1⊗⋯⊗Ek{\ displaystyle E_ {1} \ otimes \ cdots \ otimes E_ {k}} =Lk(E1∗×⋯×Ek∗,K){\ displaystyle = {\ mathcal {L}} _ {k} (E_ {1} ^ {*} \ times \ cdots \ times E_ {k} ^ {*}, \ mathbb {K})}
=Lk(E1∗×⋯×Ek∗,K){\ displaystyle = {\ mathcal {L}} _ {k} (E_ {1} ^ {*} \ times \ cdots \ times E_ {k} ^ {*}, \ mathbb {K})} Dimensiune
Dimensiune
Dimensiunea unui produs tensor al spațiilor este egală cu produsul dimensiunilor tuturor spațiilor.
Soare(E1⊗⋯⊗Ek)=Soare(E1)⋯Soare(Ek){\ displaystyle \ dim (E_ {1} \ otimes \ cdots \ otimes E_ {k}) = \ dim (E_ {1}) \ cdots \ dim (E_ {k})} Corpul scalarilor
Corpul scalarilor
K{\ displaystyle \ mathbb {K}} fiind un spațiu vectorial de dimensiunea 1 pe sine, poate fi utilizat în produsul tensor. și sunt canonic izomorfe pentru . Prin urmare, îl putem considera ca un fel de element neutru.
E⊗K{\ displaystyle E \ otimes \ mathbb {K}}
fiind un spațiu vectorial de dimensiunea 1 pe sine, poate fi utilizat în produsul tensor. și sunt canonic izomorfe pentru . Prin urmare, îl putem considera ca un fel de element neutru.
E⊗K{\ displaystyle E \ otimes \ mathbb {K}} K⊗E{\ displaystyle \ mathbb {K} \ otimes E}
K⊗E{\ displaystyle \ mathbb {K} \ otimes E} E{\ displaystyle E}
E{\ displaystyle E} K{\ displaystyle \ mathbb {K}}
K{\ displaystyle \ mathbb {K}}
E⊗K=K⊗E=E{\ displaystyle E \ otimes \ mathbb {K} = \ mathbb {K} \ otimes E = E} Puteri tensoriale
Puteri tensoriale
Putem defini puterea tensorială a unui spațiu , notată sau , prin:
k{\ displaystyle k} E{\ displaystyle E}
E{\ displaystyle E} E⊗k{\ displaystyle E ^ {\ otimes k}}
E⊗k{\ displaystyle E ^ {\ otimes k}} ⨂kE{\ displaystyle \ bigotimes _ {k} E}
⨂kE{\ displaystyle \ bigotimes _ {k} E}
- la , ;k≥2{\ displaystyle k \ geq 2}
 E⊗k=E⊗(k-1)⊗E{\ displaystyle E ^ {\ otimes k} = E ^ {\ otimes (k-1)} \ otimes E}
E⊗k=E⊗(k-1)⊗E{\ displaystyle E ^ {\ otimes k} = E ^ {\ otimes (k-1)} \ otimes E}
- pentru , prin extrapolarea definițiilor de mai sus ;k=1{\ displaystyle k = 1}
 E⊗1=L(E∗,K)=E∗∗=E{\ displaystyle E ^ {\ otimes 1} = {\ mathcal {L}} (E ^ {*}, \ mathbb {K}) = E ^ {**} = E}
E⊗1=L(E∗,K)=E∗∗=E{\ displaystyle E ^ {\ otimes 1} = {\ mathcal {L}} (E ^ {*}, \ mathbb {K}) = E ^ {**} = E}
- căci alegerea face posibilă generalizarea formulelor într-un mod coerent.k=0{\ displaystyle k = 0}
 E⊗0=K{\ displaystyle E ^ {\ otimes 0} = \ mathbb {K}}
E⊗0=K{\ displaystyle E ^ {\ otimes 0} = \ mathbb {K}}
De asemenea, avem proprietățile:
E⊗k⊗E⊗l=E⊗(k+l){\ displaystyle E ^ {\ otimes k} \ otimes E ^ {\ otimes l} = E ^ {\ otimes (k + l)}} (E⊗k)⊗l=E⊗(kl){\ displaystyle (E ^ {\ otimes k}) ^ {\ otimes l} = E ^ {\ otimes (kl)}}
(E⊗k)⊗l=E⊗(kl){\ displaystyle (E ^ {\ otimes k}) ^ {\ otimes l} = E ^ {\ otimes (kl)}} Dualitate
Dualitate
Încă o dată prin izomorfism canonic avem: (E1⊗⋯⊗Ek)∗{\ displaystyle (E_ {1} \ otimes \ cdots \ otimes E_ {k}) ^ {*}} =E1∗⊗⋯⊗Ek∗{\ displaystyle = E_ {1} ^ {*} \ otimes \ cdots \ otimes E_ {k} ^ {*}}
=E1∗⊗⋯⊗Ek∗{\ displaystyle = E_ {1} ^ {*} \ otimes \ cdots \ otimes E_ {k} ^ {*}}
Spații de aplicare liniare și multiliniare
Spațiul vectorial al hărților liniare din in este canonic izomorf la . Mai general, aplicațiile spațiale ale lui k- linéaires sunt în mod canonic izomorfe . Prin urmare, este posibil să confundăm aceste spații.
L(E,F){\ displaystyle {\ mathcal {L}} (E, F)} E{\ displaystyle E}
E{\ displaystyle E} F{\ displaystyle F}
F{\ displaystyle F} F⊗E∗{\ displaystyle F \ otimes E ^ {*}}
F⊗E∗{\ displaystyle F \ otimes E ^ {*}} E1×⋯×Ek{\ displaystyle E_ {1} \ times \ cdots \ times E_ {k}}
E1×⋯×Ek{\ displaystyle E_ {1} \ times \ cdots \ times E_ {k}} F{\ displaystyle F}
F{\ displaystyle F} F⊗E1∗⊗⋯⊗Ek∗{\ displaystyle F \ otimes E_ {1} ^ {*} \ otimes \ cdots \ otimes E_ {k} ^ {*}}
F⊗E1∗⊗⋯⊗Ek∗{\ displaystyle F \ otimes E_ {1} ^ {*} \ otimes \ cdots \ otimes E_ {k} ^ {*}}
Despre comutativitate
Există un izomorfism între și . În practică, asimilarea lor (adică a le face comutative) nu este totuși un lucru bun, totuși. Acest lucru este deosebit de problematic atunci când . Într-adevăr, această asimilare ar putea, în acest caz, să ducă la convingerea că produsul tensor al a două elemente (descris mai jos) este comutativ, ceea ce nu este cazul.
E⊗F{\ displaystyle E \ otimes F} F⊗E{\ displaystyle F \ otimes E}
F⊗E{\ displaystyle F \ otimes E} ⊗{\ displaystyle \ otimes}
⊗{\ displaystyle \ otimes} E=F{\ displaystyle E = F}
E=F{\ displaystyle E = F}
Prin urmare, în restul acestui articol vom considera, dacă nu se specifică altfel, și ca două spații distincte. Considerațiile legate de izomorfismele lor sunt discutate în această secțiune .
E⊗F{\ displaystyle E \ otimes F} F⊗E{\ displaystyle F \ otimes E}
F⊗E{\ displaystyle F \ otimes E}
Tensori și produs tensor pe elemente
Interesul principal al produsului tensorial este de a defini o operație pe vectori (sau mai general elementele modulelor ) având proprietăți similare cu cele ale unui produs. Acestea fiind spuse, spre deosebire de produsele obișnuite, produsul tensor nu este o operație internă: poate fi realizat pe vectori care rezultă din diferite spații vectoriale și rezultatul său (cu câteva excepții) nu aparține niciunui dintre spațiile în cauză. Elementele implicate în astfel de produse se numesc tensori .
Definiție
Fie și să fie două forme liniare. Rețineți aplicația definită de:
ϕ∈E∗{\ displaystyle \ phi \ în E ^ {*}} ψ∈F∗{\ displaystyle \ psi \ în F ^ {*}}
ψ∈F∗{\ displaystyle \ psi \ în F ^ {*}} ϕ⊗ψ{\ displaystyle \ phi \ otimes \ psi}
ϕ⊗ψ{\ displaystyle \ phi \ otimes \ psi}
∀tu∈E,∀v∈F,(ϕ⊗ψ)(tu,v)=ϕ(tu)⋅ψ(v){\ displaystyle \ forall u \ in E, \ forall v \ in F, (\ phi \ otimes \ psi) (u, v) = \ phi (u) \ cdot \ psi (v)}
Este o formă biliniară: de aceea avem . Produsul se generalizează ușor la forme multiliniare.
ϕ⊗ψ∈E∗⊗F∗{\ displaystyle \ phi \ otimes \ psi \ în E ^ {*} \ otimes F ^ {*}}
Ca și în dimensiunea finită , orice vector (respectiv ) poate fi asemănat cu o formă liniară pe (respectiv ). Astfel, definim în general produsul tensorial al și , notat ca o formă biliniară pe .
E=E∗∗{\ displaystyle E = E ^ {**}} tu{\ displaystyle u}
tu{\ displaystyle u} v{\ displaystyle v}
v{\ displaystyle v} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}} F∗{\ displaystyle F ^ {*}}
F∗{\ displaystyle F ^ {*}} tu{\ displaystyle u}
tu{\ displaystyle u} v{\ displaystyle v}
v{\ displaystyle v} tu⊗v{\ displaystyle u \ otimes v}
tu⊗v{\ displaystyle u \ otimes v} E∗×F∗{\ displaystyle E ^ {*} \ times F ^ {*}}
E∗×F∗{\ displaystyle E ^ {*} \ times F ^ {*}}
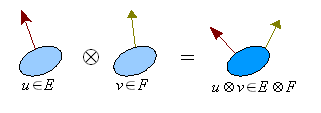
Forma biliniară este deci un tensor aparținând . Forma biliniară este la rândul său un tensor aparținând . Tensorul poate fi definită (în dimensiune finită) ca forme multiliniare furnizate împreună cu produsul .
ϕ⊗ψ{\ displaystyle \ phi \ otimes \ psi} E∗⊗F∗{\ displaystyle E ^ {*} \ otimes F ^ {*}}
E∗⊗F∗{\ displaystyle E ^ {*} \ otimes F ^ {*}} tu⊗v{\ displaystyle u \ otimes v}
tu⊗v{\ displaystyle u \ otimes v} E⊗F{\ displaystyle E \ otimes F}
E⊗F{\ displaystyle E \ otimes F} ⊗{\ displaystyle \ otimes}
⊗{\ displaystyle \ otimes}
Observații
- În schimb, orice tensor nu este neapărat scris ca produs . Pe de altă parte, poate fi întotdeauna descompus într- o combinație liniară de elemente ale formei unde și . Adică, se pot găsi întotdeauna familii de vectori și și o familie de scalari precum .T∈E⊗F{\ displaystyle T \ in E \ otimes F}
 T=tu⊗v{\ displaystyle T = u \ otimes v}
T=tu⊗v{\ displaystyle T = u \ otimes v} tueu⊗vj{\ displaystyle u_ {i} \ otimes v_ {j}}
tueu⊗vj{\ displaystyle u_ {i} \ otimes v_ {j}} tueu∈E{\ displaystyle u_ {i} \ în E}
tueu∈E{\ displaystyle u_ {i} \ în E} vj∈F{\ displaystyle v_ {j} \ în F}
vj∈F{\ displaystyle v_ {j} \ în F} (tueu)eu{\ displaystyle (u_ {i}) _ {i}}
(tueu)eu{\ displaystyle (u_ {i}) _ {i}} (vj)j{\ displaystyle (v_ {j}) _ {j}}
(vj)j{\ displaystyle (v_ {j}) _ {j}} (Teuj)euj{\ displaystyle (T_ {ij}) _ {ij}}
(Teuj)euj{\ displaystyle (T_ {ij}) _ {ij}} T=∑eu,jTeuj⋅tueu⊗vj{\ displaystyle T = \ sum _ {i, j} T_ {ij} \ cdot u_ {i} \ otimes v_ {j}}
T=∑eu,jTeuj⋅tueu⊗vj{\ displaystyle T = \ sum _ {i, j} T_ {ij} \ cdot u_ {i} \ otimes v_ {j}}
- Se observă că orice vector este un anumit tip de tensor (este întotdeauna comparabil cu o formă 1-liniară) și că orice tensor face parte dintr-un spațiu vectorial. Utilizarea termenului tensor implică utilizarea produsului tensor. În practică, termenul tensor este utilizat în principal în ceea ce privește produsele vectorilor din același spațiu sau ale dualului său .E{\ displaystyle E}
 E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}}
Proprietățile produsului tensor
Asociativitate
Datorită izomorfismului canonic putem considera că produsul tensor este asociativ. Cu alte cuvinte . De asemenea , se arată tensor ca formă tri liniar: . Într-un mod general, dacă cineva își dă vectori , tensorul este un element al . Prin urmare, este o formă liniară.
(tu⊗v)⊗w=tu⊗(v⊗w){\ displaystyle (u \ otimes v) \ otimes w = u \ otimes (v \ otimes w)} tu⊗v⊗w{\ displaystyle u \ otimes v \ otimes w}
tu⊗v⊗w{\ displaystyle u \ otimes v \ otimes w} (tu⊗v⊗w)(X,y,z)=tu(X)⋅v(y)⋅w(z){\ displaystyle (u \ otimes v \ otimes w) (x, y, z) = u (x) \ cdot v (y) \ cdot w (z)}
(tu⊗v⊗w)(X,y,z)=tu(X)⋅v(y)⋅w(z){\ displaystyle (u \ otimes v \ otimes w) (x, y, z) = u (x) \ cdot v (y) \ cdot w (z)} k{\ displaystyle k}
k{\ displaystyle k} tueu∈Eeu{\ displaystyle u_ {i} \ în E_ {i}}
tueu∈Eeu{\ displaystyle u_ {i} \ în E_ {i}} tu1⊗⋯⊗tuk{\ displaystyle u_ {1} \ otimes \ cdots \ otimes u_ {k}}
tu1⊗⋯⊗tuk{\ displaystyle u_ {1} \ otimes \ cdots \ otimes u_ {k}} E1⊗⋯⊗Ek{\ displaystyle E_ {1} \ otimes \ cdots \ otimes E_ {k}}
E1⊗⋯⊗Ek{\ displaystyle E_ {1} \ otimes \ cdots \ otimes E_ {k}} k{\ displaystyle k}
k{\ displaystyle k}
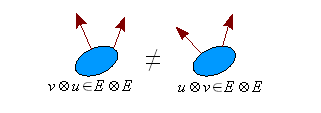
 Non-comutativitate
Non-comutativitate
Dacă și , tensorii și apoi ambii aparțin aceluiași spațiu . Cu toate acestea, vom avea grijă să observăm că în cazul general .
tu∈E{\ displaystyle u \ in E} v∈E{\ displaystyle v \ în E}
v∈E{\ displaystyle v \ în E} tu⊗v{\ displaystyle u \ otimes v}
tu⊗v{\ displaystyle u \ otimes v} v⊗tu{\ displaystyle v \ otimes u}
v⊗tu{\ displaystyle v \ otimes u} E⊗E{\ displaystyle E \ otimes E}
E⊗E{\ displaystyle E \ otimes E} tu⊗v≠v⊗tu{\ displaystyle u \ otimes v \ neq v \ otimes u}
tu⊗v≠v⊗tu{\ displaystyle u \ otimes v \ neq v \ otimes u}
 Distributivitate
Distributivitate
Produsul tensor se comportă bine ca un produs în ceea ce privește adăugarea de spații vectoriale:
(tu+tu′)⊗v=tu⊗v+tu′⊗v{\ displaystyle (u + u ') \ otimes v = u \ otimes v + u' \ otimes v} tu⊗(v+v′)=tu⊗v+tu⊗v′{\ displaystyle u \ otimes (v + v ') = u \ otimes v + u \ otimes v'}
tu⊗(v+v′)=tu⊗v+tu⊗v′{\ displaystyle u \ otimes (v + v ') = u \ otimes v + u \ otimes v'} Generalizarea produselor uzuale
Generalizarea produselor uzuale
Rețineți că produsul tensor generalizează produsul printr-un scalar definit pe spațiile -vector precum și produsul din câmp . Avem astfel și .
K{\ displaystyle \ mathbb {K}} (E,K,+,⋅){\ displaystyle (E, \ mathbb {K}, +, \ cdot)}
(E,K,+,⋅){\ displaystyle (E, \ mathbb {K}, +, \ cdot)} (K,+,×){\ displaystyle (\ mathbb {K}, +, \ times)}
(K,+,×){\ displaystyle (\ mathbb {K}, +, \ times)} λ⊗tu=λ⋅tu{\ displaystyle \ lambda \ otimes u = \ lambda \ cdot u}
λ⊗tu=λ⋅tu{\ displaystyle \ lambda \ otimes u = \ lambda \ cdot u} λ1⊗λ2=λ1×λ2{\ displaystyle \ lambda _ {1} \ otimes \ lambda _ {2} = \ lambda _ {1} \ times \ lambda _ {2}}
λ1⊗λ2=λ1×λ2{\ displaystyle \ lambda _ {1} \ otimes \ lambda _ {2} = \ lambda _ {1} \ times \ lambda _ {2}}
 Bazele domeniilor de produse
Bazele domeniilor de produse
Fie o bază și o bază a . Deci familia formează o bază a . În consecință, orice element admite o singură familie de coordonate pe această bază:
(e1,e2,⋯,enu){\ displaystyle (e_ {1}, e_ {2}, \ cdots, e_ {n})} E{\ displaystyle E}
E{\ displaystyle E} (ϵ1,ϵ2,...ϵm){\ displaystyle (\ epsilon _ {1}, \ epsilon _ {2}, ... \ epsilon _ {m})}
(ϵ1,ϵ2,...ϵm){\ displaystyle (\ epsilon _ {1}, \ epsilon _ {2}, ... \ epsilon _ {m})} F{\ displaystyle F}
F{\ displaystyle F} (eeu⊗ϵj)1≤eu≤nu,1≤j≤m{\ displaystyle (e_ {i} \ otimes \ epsilon _ {j}) _ {1 \ leq i \ leq n, 1 \ leq j \ leq m}}
(eeu⊗ϵj)1≤eu≤nu,1≤j≤m{\ displaystyle (e_ {i} \ otimes \ epsilon _ {j}) _ {1 \ leq i \ leq n, 1 \ leq j \ leq m}} E⊗F{\ displaystyle E \ otimes F}
E⊗F{\ displaystyle E \ otimes F} T∈E⊗F{\ displaystyle T \ in E \ otimes F}
T∈E⊗F{\ displaystyle T \ in E \ otimes F}
∃!(Teuj)euj∈Knum,T=∑eu=1nu∑j=1mTeuj⋅eeu⊗ϵj{\ displaystyle \ există! (T_ {ij}) _ {ij} \ in \ mathbb {K} ^ {nm}, T = \ sum _ {i = 1} ^ {n} \ sum _ {j = 1} ^ {m} T_ {ij} \ cdot e_ {i} \ otimes \ epsilon _ {j}}
Această formulă este destul de consistentă cu faptul că . Coordonatele pot fi calculate în mod explicit folosind bazele duale și prin formula:
Soare(E⊗F)=Soare(E)⋅Soare(F){\ displaystyle \ dim (E \ otimes F) = \ dim (E) \ cdot \ dim (F)} (Teuj)euj{\ displaystyle (T_ {ij}) _ {ij}}
(Teuj)euj{\ displaystyle (T_ {ij}) _ {ij}} (e1∗,e2∗,⋯,enu∗){\ displaystyle (e_ {1} ^ {*}, e_ {2} ^ {*}, \ cdots, e_ {n} ^ {*})}
(e1∗,e2∗,⋯,enu∗){\ displaystyle (e_ {1} ^ {*}, e_ {2} ^ {*}, \ cdots, e_ {n} ^ {*})} (ϵ1∗,ϵ2∗,...ϵm∗){\ displaystyle (\ epsilon _ {1} ^ {*}, \ epsilon _ {2} ^ {*}, ... \ epsilon _ {m} ^ {*})}
(ϵ1∗,ϵ2∗,...ϵm∗){\ displaystyle (\ epsilon _ {1} ^ {*}, \ epsilon _ {2} ^ {*}, ... \ epsilon _ {m} ^ {*})}
∀eu,∀j,Teuj=T(eeu∗,ϵj∗){\ displaystyle \ forall i, \ forall j, \ quad T_ {ij} = T (e_ {i} ^ {*}, \ epsilon _ {j} ^ {*})}
Aceste formule sunt generalizate pentru spațiile vectoriale.
k{\ displaystyle k}
Operațiune de contracție
Definiție
Fie un spațiu vectorial dimensional finit peste un câmp astfel încât . Se presupune că există doi indici și astfel încât (sau într-o manieră complet echivalentă ). Fie o bază a ; baza duală este deci o bază a . Având în vedere un tensor , aplicația
E{\ displaystyle {\ mathcal {E}}} K{\ displaystyle \ mathbb {K}}
K{\ displaystyle \ mathbb {K}} E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}}
E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}} eu{\ displaystyle i}
eu{\ displaystyle i} j{\ displaystyle j}
j{\ displaystyle j} Eeu=Ej∗{\ displaystyle E_ {i} = E_ {j} ^ {*}}
Eeu=Ej∗{\ displaystyle E_ {i} = E_ {j} ^ {*}} Ej=Eeu∗{\ displaystyle E_ {j} = E_ {i} ^ {*}}
Ej=Eeu∗{\ displaystyle E_ {j} = E_ {i} ^ {*}} (e1,e2,⋯,enu){\ displaystyle (e_ {1}, e_ {2}, \ cdots, e_ {n})}
(e1,e2,⋯,enu){\ displaystyle (e_ {1}, e_ {2}, \ cdots, e_ {n})} Eeu{\ displaystyle E_ {i}}
Eeu{\ displaystyle E_ {i}} (e1∗,e2∗,⋯,enu∗){\ displaystyle (e_ {1} ^ {*}, e_ {2} ^ {*}, \ cdots, e_ {n} ^ {*})}
(e1∗,e2∗,⋯,enu∗){\ displaystyle (e_ {1} ^ {*}, e_ {2} ^ {*}, \ cdots, e_ {n} ^ {*})} Ej{\ displaystyle E_ {j}}
Ej{\ displaystyle E_ {j}} T∈E{\ displaystyle T \ in {\ mathcal {E}}}
T∈E{\ displaystyle T \ in {\ mathcal {E}}}
(tu1,⋯,tueu-1,tueu+1,⋯,tuj-1,tuj+1,⋯,tuk)↦∑r=1nuT(tu1,⋯,tueu-1,er∗,tueu+1,⋯,tuj-1,er,tuj+1,⋯,tuk){\ displaystyle (u_ {1}, \ cdots, u_ {i-1}, u_ {i + 1}, \ cdots, u_ {j-1}, u_ {j + 1}, \ cdots, u_ {k} ) \ mapsto \ sum _ {r = 1} ^ {n} T (u_ {1}, \ cdots, u_ {i-1}, e_ {r} ^ {*}, u_ {i + 1}, \ cdots , u_ {j-1}, e_ {r}, u_ {j + 1}, \ cdots, u_ {k})}
este o formă -liniară pe , cu alte cuvinte un tensor de . De asemenea , această formă este independentă de alegerea bazei de . Operația se numește contracția de pe indici și . Uneori se remarcă(k-2){\ displaystyle (k-2)} E1∗×⋯×Eeu-1∗×Eeu+1∗×⋯×Ej-1∗×Ej+1∗×⋯×Ek∗{\ displaystyle E_ {1} ^ {*} \ times \ cdots \ times E_ {i-1} ^ {*} \ times E_ {i + 1} ^ {*} \ times \ cdots \ times E_ {j-1 } ^ {*} \ times E_ {j + 1} ^ {*} \ times \ cdots \ times E_ {k} ^ {*}}
E1∗×⋯×Eeu-1∗×Eeu+1∗×⋯×Ej-1∗×Ej+1∗×⋯×Ek∗{\ displaystyle E_ {1} ^ {*} \ times \ cdots \ times E_ {i-1} ^ {*} \ times E_ {i + 1} ^ {*} \ times \ cdots \ times E_ {j-1 } ^ {*} \ times E_ {j + 1} ^ {*} \ times \ cdots \ times E_ {k} ^ {*}} E1⊗⋯⊗Eeu-1⊗Eeu+1⊗⋯⊗Ej-1⊗Ej+1⊗⋯⊗Ek{\ displaystyle E_ {1} \ otimes \ cdots \ otimes E_ {i-1} \ otimes E_ {i + 1} \ otimes \ cdots \ otimes E_ {j-1} \ otimes E_ {j + 1} \ otimes \ cdots \ otimes E_ {k}}
E1⊗⋯⊗Eeu-1⊗Eeu+1⊗⋯⊗Ej-1⊗Ej+1⊗⋯⊗Ek{\ displaystyle E_ {1} \ otimes \ cdots \ otimes E_ {i-1} \ otimes E_ {i + 1} \ otimes \ cdots \ otimes E_ {j-1} \ otimes E_ {j + 1} \ otimes \ cdots \ otimes E_ {k}} Eeu{\ displaystyle E_ {i}}
Eeu{\ displaystyle E_ {i}} T{\ displaystyle T}
T{\ displaystyle T} eu{\ displaystyle i}
eu{\ displaystyle i} j{\ displaystyle j}
j{\ displaystyle j} treuj{\ displaystyle \ mathrm {tr} _ {ij}}
treuj{\ displaystyle \ mathrm {tr} _ {ij}}
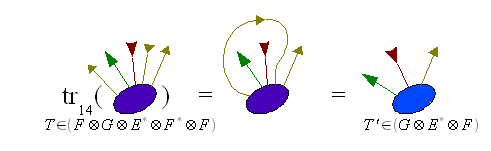
Este important să rețineți că operațiunea de contracție este posibilă numai pentru doi indici care corespund unor spații duale între ele și nu are sens în alte cazuri. Este, de asemenea, o operație liniară de in .
E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}} F=E1⊗⋯⊗Eeu-1⊗Eeu+1⊗⋯⊗Ej-1⊗Ej+1⊗⋯⊗Ek{\ displaystyle {\ mathcal {F}} = E_ {1} \ otimes \ cdots \ otimes E_ {i-1} \ otimes E_ {i + 1} \ otimes \ cdots \ otimes E_ {j-1} \ otimes E_ {j + 1} \ otimes \ cdots \ otimes E_ {k}}
F=E1⊗⋯⊗Eeu-1⊗Eeu+1⊗⋯⊗Ej-1⊗Ej+1⊗⋯⊗Ek{\ displaystyle {\ mathcal {F}} = E_ {1} \ otimes \ cdots \ otimes E_ {i-1} \ otimes E_ {i + 1} \ otimes \ cdots \ otimes E_ {j-1} \ otimes E_ {j + 1} \ otimes \ cdots \ otimes E_ {k}}
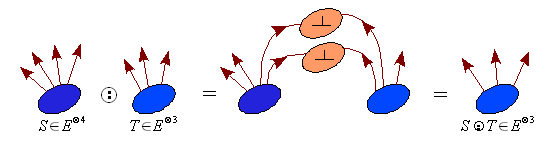
Produs contractat
În practică, contracția este adesea utilizată în cadrul unei operațiuni numite produs contractat și notată , sau chiar pur și simplu . Produsul contractat a doi tensori este rezultatul produsului tensorial al acestora urmat de o contracție a unui indice al primului de un indice al celui de-al doilea. Rețineți că notațiile sunt incomplete: nu specifică care sunt indicii de contracție. În mod implicit, este, în general, ultimul index al primului tensor și primul index al celui de-al doilea. În ceea ce privește contracția, produsul contractat are semnificație numai dacă indicii contractați corespund spațiilor duale.
⊙{\ displaystyle \ odot} ⊗¯{\ displaystyle {\ bar {\ otimes}}}
⊗¯{\ displaystyle {\ bar {\ otimes}}} ⋅{\ displaystyle \ cdot}
⋅{\ displaystyle \ cdot}

Proprietățile produsului contractat
Asociativitate
Produsul contractat este asociativ dacă tensorul centrului are cel puțin doi indici. Deci pentru , și , avem . Dacă tensorul centrului are un singur index, este posibil ca una dintre cele două paranteze să nu aibă o direcție și chiar și în caz contrar, egalitatea nu se va realiza în cazul general.
R∈E⊗⋯⊗F∗{\ displaystyle R \ in E \ otimes \ cdots \ otimes F ^ {*}} S∈F⊗⋯⊗G∗{\ displaystyle S \ in F \ otimes \ cdots \ otimes G ^ {*}}
S∈F⊗⋯⊗G∗{\ displaystyle S \ in F \ otimes \ cdots \ otimes G ^ {*}} T∈G⊗⋯⊗H∗{\ displaystyle T \ in G \ otimes \ cdots \ otimes H ^ {*}}
T∈G⊗⋯⊗H∗{\ displaystyle T \ in G \ otimes \ cdots \ otimes H ^ {*}} (R⊙S)⊙T=R⊙(S⊙T){\ displaystyle (R \ odot S) \ odot T = R \ odot (S \ odot T)}
(R⊙S)⊙T=R⊙(S⊙T){\ displaystyle (R \ odot S) \ odot T = R \ odot (S \ odot T)}
Distributivitate
Produsul contractat se comportă bine ca un produs față de adăugarea de spații vectoriale:
(S+S′)⊙T=S⊙T+S′⊙T{\ displaystyle (S + S ') \ odot T = S \ odot T + S' \ odot T} S⊙(T+T′)=S⊙T+S⊙T′{\ displaystyle S \ odot (T + T ') = S \ odot T + S \ odot T'}
S⊙(T+T′)=S⊙T+S⊙T′{\ displaystyle S \ odot (T + T ') = S \ odot T + S \ odot T'} Imagine după tensor sau produs contractat
Imagine după tensor sau produs contractat
Având în vedere un tensor și vectori astfel încât să putem efectua două operații:
T∈E1∗⊗⋯⊗Ek∗{\ displaystyle T \ in E_ {1} ^ {*} \ otimes \ cdots \ otimes E_ {k} ^ {*}} k{\ displaystyle k}
k{\ displaystyle k} veu∈Eeu{\ displaystyle v_ {i} \ în E_ {i}}
veu∈Eeu{\ displaystyle v_ {i} \ în E_ {i}}
- calcularea imaginii vectorilor (care, ne reamintim, poate fi întotdeauna văzută ca o formă multiliniară) ;k{\ displaystyle k}
 T{\ displaystyle T}
T{\ displaystyle T} T(v1,⋯,vk){\ displaystyle T (v_ {1}, \ cdots, v_ {k})}
T(v1,⋯,vk){\ displaystyle T (v_ {1}, \ cdots, v_ {k})}
- calculați produsele contractate succesive ale fiecărui vector .T{\ displaystyle T}
 ((⋯(T⊙vk)⋯)⊙v2)⊙v1{\ displaystyle ((\ cdots (T \ odot v_ {k}) \ cdots) \ odot v_ {2}) \ odot v_ {1}}
((⋯(T⊙vk)⋯)⊙v2)⊙v1{\ displaystyle ((\ cdots (T \ odot v_ {k}) \ cdots) \ odot v_ {2}) \ odot v_ {1}}
Este de fapt o singură operație: T(v1,⋯,vk)=((⋯(T⊙vk)⋯)⊙v2)⊙v1{\ displaystyle T (v_ {1}, \ cdots, v_ {k}) = ((\ cdots (T \ odot v_ {k}) \ cdots) \ odot v_ {2}) \ odot v_ {1}}

Mai general, în cazul în care tensorul construită prin evaluarea poziției de -lea este egal cu produsul contractat de la ei indicelui -lea prin indexul său unic. De atunci devine posibilă ascunderea completă a aspectului funcțional al luării în considerare numai a proprietăților sale algebrice.
tu∈Eeu{\ displaystyle u \ in E_ {i}} (v1,⋯,veu-1,veu+1,⋯,vk)↦T(v1,⋯,veu-1,tu,veu+1,⋯,vk){\ displaystyle (v_ {1}, \ cdots, v_ {i-1}, v_ {i + 1}, \ cdots, v_ {k}) \ mapsto T (v_ {1}, \ cdots, v_ {i- 1}, u, v_ {i + 1}, \ cdots, v_ {k})}
(v1,⋯,veu-1,veu+1,⋯,vk)↦T(v1,⋯,veu-1,tu,veu+1,⋯,vk){\ displaystyle (v_ {1}, \ cdots, v_ {i-1}, v_ {i + 1}, \ cdots, v_ {k}) \ mapsto T (v_ {1}, \ cdots, v_ {i- 1}, u, v_ {i + 1}, \ cdots, v_ {k})} eu{\ displaystyle i}
eu{\ displaystyle i} T{\ displaystyle T}
T{\ displaystyle T} T{\ displaystyle T}
T{\ displaystyle T} eu{\ displaystyle i}
eu{\ displaystyle i} tu{\ displaystyle u}
tu{\ displaystyle u} T{\ displaystyle T}
T{\ displaystyle T}
Cârlig de dualitate
Cârligul dualitate este un caz special de produs contractat: .
⟨ϕ,tu⟩=ϕ⊙tu{\ displaystyle \ langle \ phi, u \ rangle = \ phi \ odot u}
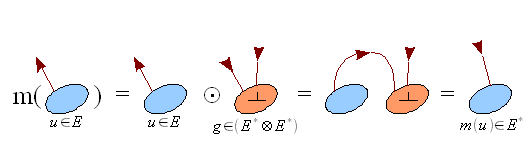
 Imagine prin aplicație liniară
Imagine prin aplicație liniară
Deoarece aplicația liniară poate fi văzută ca un tensor , putem calcula imaginea unui vector ca fiind produsul contractat .
f:E→F{\ displaystyle f: E \ rightarrow F} T∈F⊗E∗{\ displaystyle T \ in F \ otimes E ^ {*}}
T∈F⊗E∗{\ displaystyle T \ in F \ otimes E ^ {*}} tu∈E{\ displaystyle u \ in E}
tu∈E{\ displaystyle u \ in E} T⊙tu=f(tu){\ displaystyle T \ odot u = f (u)}
T⊙tu=f(tu){\ displaystyle T \ odot u = f (u)}
Compus din aplicații liniare
Dacă și sunt reprezentate de tensori și , atunci harta compusă poate fi reprezentată de tensor .
f:E→F{\ displaystyle f: E \ rightarrow F} g:F→G{\ displaystyle g: F \ rightarrow G}
g:F→G{\ displaystyle g: F \ rightarrow G} T∈F⊗E∗{\ displaystyle T \ in F \ otimes E ^ {*}}
T∈F⊗E∗{\ displaystyle T \ in F \ otimes E ^ {*}} S∈G⊗F∗{\ displaystyle S \ in G \ otimes F ^ {*}}
S∈G⊗F∗{\ displaystyle S \ in G \ otimes F ^ {*}} g∘f:E→G{\ displaystyle g \ circ f: E \ rightarrow G}
g∘f:E→G{\ displaystyle g \ circ f: E \ rightarrow G} S⊙T{\ displaystyle S \ odot T}
S⊙T{\ displaystyle S \ odot T}
Produsul a fost contractat de mai multe ori
Contracția poate fi exercitată de mai multe ori în urma unui produs tensor. De exemplu, produsul dublu contractat (notat , sau prin două puncte într - un cerc) corespunde două contracții succesive după un produs tensor. Aici, din nou, indicii de contracție nu sunt în general precizați, produsul dublu contractat corespunde adesea contracției ultimului indice de către primul și a penultimului cu cel de-al doilea .
:{\ displaystyle:} ⊗¯¯{\ displaystyle {\ bar {\ bar {\ otimes}}}}
⊗¯¯{\ displaystyle {\ bar {\ bar {\ otimes}}}} S⊗¯¯T{\ displaystyle S {\ bar {\ bar {\ otimes}}} T}
S⊗¯¯T{\ displaystyle S {\ bar {\ bar {\ otimes}}} T} S{\ displaystyle S}
S{\ displaystyle S} T{\ displaystyle T}
T{\ displaystyle T} S{\ displaystyle S}
S{\ displaystyle S} T{\ displaystyle T}
T{\ displaystyle T}

Se poate defini în același mod un produs odată contractat dacă tensorii o permit.
nu{\ displaystyle n}
Permutarea indicilor
Spațiile și pot fi legate printr-un izomorfism care constă pur și simplu în inversarea ordinii indicilor. Astfel, la orice putem asocia un singur element , pe care îl vom nota , cum ar fi:
E⊗F{\ displaystyle E \ otimes F} F⊗E{\ displaystyle F \ otimes E}
F⊗E{\ displaystyle F \ otimes E} T∈E⊗F{\ displaystyle T \ in E \ otimes F}
T∈E⊗F{\ displaystyle T \ in E \ otimes F} F⊗E{\ displaystyle F \ otimes E}
F⊗E{\ displaystyle F \ otimes E} τ(12)T{\ displaystyle \ tau _ {(12)} T}
τ(12)T{\ displaystyle \ tau _ {(12)} T}
∀tu∈E∗,∀v∈F∗,[τ(12)T](v,tu)=T(tu,v){\ displaystyle \ forall u \ in E ^ {*}, \ forall v \ in F ^ {*}, \ quad \ left [\ tau _ {(12)} T \ right] (v, u) = T ( u, v)}![\ forall u \ in E ^ {*}, \ forall v \ in F ^ {*}, \ quad \ left [\ tau _ {{(12)}} T \ right] (v, u) = T (u , v)](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d9f7d9c4b082516dd90b4943ea2bc896cec8ce4)
Acest principiu este generalizat pentru spații. Fie un spațiu vectorial dimensional finit peste un câmp și o permutare . Putem defini un izomorfism care are orice element de asociați un tensor de , definit prin:
k{\ displaystyle k} E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}}
E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}} K{\ displaystyle \ mathbb {K}}
K{\ displaystyle \ mathbb {K}} σ∈Sk{\ displaystyle \ sigma \ in {\ mathfrak {S}} _ {k}}
σ∈Sk{\ displaystyle \ sigma \ in {\ mathfrak {S}} _ {k}} τσ{\ displaystyle \ tau _ {\ sigma}}
τσ{\ displaystyle \ tau _ {\ sigma}} T{\ displaystyle T}
T{\ displaystyle T} E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}}
E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}} τσT{\ displaystyle \ tau _ {\ sigma} T}
τσT{\ displaystyle \ tau _ {\ sigma} T} F=Eσ(1)⊗⋯⊗Eσ(k){\ displaystyle {\ mathcal {F}} = E _ {\ sigma (1)} \ otimes \ cdots \ otimes E _ {\ sigma (k)}}
F=Eσ(1)⊗⋯⊗Eσ(k){\ displaystyle {\ mathcal {F}} = E _ {\ sigma (1)} \ otimes \ cdots \ otimes E _ {\ sigma (k)}}
∀veu∈Eeu∗,[τσT](vσ(1),⋯,vσ(k))=T(v1,⋯,vk){\ displaystyle \ forall v_ {i} \ în E_ {i} ^ {*}, \ quad \ left [\ tau _ {\ sigma} T \ right] (v _ {\ sigma (1)}, \ cdots, v_ {\ sigma (k)}) = T (v_ {1}, \ cdots, v_ {k})}![\ forall v_ {i} \ în E_ {i} ^ {*}, \ quad \ left [\ tau _ {\ sigma} T \ right] (v _ {{\ sigma (1)}}, \ cdots, v_ {{\ sigma (k)}}) = T (v_ {1}, \ cdots, v_ {k})](https://wikimedia.org/api/rest_v1/media/math/render/svg/679dec6d2519ffcad4063b85982329f207814922)
Putem vedea clar că o permutare induce în mod natural un izomorfism între spații și .
E{\ displaystyle {\ mathcal {E}}} F{\ displaystyle {\ mathcal {F}}}
F{\ displaystyle {\ mathcal {F}}}
Din motive de comoditate, putem folosi notația canonică a permutațiilor constând în indicarea numai a listei diferitelor permutații circulare. Astfel, aplicația transformă indexul 1 în indexul 2, indexul 2 în indexul 5, indexul 5 în indexul 1 și lasă ceilalți indici invarianți.
τ(125){\ displaystyle \ tau _ {(125)}}
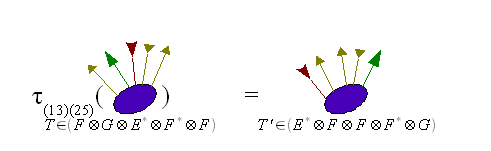
În teoria categoriilor, acest tip de aplicație, care oferă o noțiune apropiată de comutativitate, este studiat în cadrul categoriilor monoidale împletite .
Non-unicitatea izomorfismului
Pentru spații și date a priori, existența unei astfel de aplicații nu implică neapărat unicitatea acesteia. Să presupunem, de fapt, că un spațiu este prezent de mai multe ori în produs . Dacă spațiul este produsul aceluiași (dar într-o ordine posibil diferită), există mai multe permutări, astfel încât să fie un izomorfism al in . Deci , pentru și pot fi folosite ca aplicații de izomorfism , , , , și .
E{\ displaystyle {\ mathcal {E}}} F{\ displaystyle {\ mathcal {F}}}
F{\ displaystyle {\ mathcal {F}}} τ{\ displaystyle \ tau}
τ{\ displaystyle \ tau} Eeu{\ displaystyle E_ {i}}
Eeu{\ displaystyle E_ {i}} E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}}
E=E1⊗⋯⊗Ek{\ displaystyle {\ mathcal {E}} = E_ {1} \ otimes \ cdots \ otimes E_ {k}} F{\ displaystyle {\ mathcal {F}}}
F{\ displaystyle {\ mathcal {F}}} Eeu{\ displaystyle E_ {i}}
Eeu{\ displaystyle E_ {i}} σ{\ displaystyle \ sigma}
σ{\ displaystyle \ sigma} τσ{\ displaystyle \ tau _ {\ sigma}}
τσ{\ displaystyle \ tau _ {\ sigma}} E{\ displaystyle {\ mathcal {E}}}
E{\ displaystyle {\ mathcal {E}}} F{\ displaystyle {\ mathcal {F}}}
F{\ displaystyle {\ mathcal {F}}} E=E⊗F⊗E⊗E{\ displaystyle {\ mathcal {E}} = E \ otimes F \ otimes E \ otimes E}
E=E⊗F⊗E⊗E{\ displaystyle {\ mathcal {E}} = E \ otimes F \ otimes E \ otimes E} F=E⊗E⊗F⊗E{\ displaystyle {\ mathcal {F}} = E \ otimes E \ otimes F \ otimes E}
F=E⊗E⊗F⊗E{\ displaystyle {\ mathcal {F}} = E \ otimes E \ otimes F \ otimes E} τ(23){\ displaystyle \ tau _ {(23)}}
τ(23){\ displaystyle \ tau _ {(23)}} τ(1234){\ displaystyle \ tau _ {(1234)}}
τ(1234){\ displaystyle \ tau _ {(1234)}} τ(14)(23){\ displaystyle \ tau _ {(14) (23)}}
τ(14)(23){\ displaystyle \ tau _ {(14) (23)}} τ(234){\ displaystyle \ tau _ {(234)}}
τ(234){\ displaystyle \ tau _ {(234)}} τ(123){\ displaystyle \ tau _ {(123)}}
τ(123){\ displaystyle \ tau _ {(123)}} τ(1423){\ displaystyle \ tau _ {(1423)}}
τ(1423){\ displaystyle \ tau _ {(1423)}}
E⊗E{\ displaystyle E \ otimes E} poate fi legat de sine prin două permutări: identitate și aplicație . Generalizând orice ordine, spațiul poate fi prevăzut cu un grup de automorfisme alcătuite din astfel de mapări. Acest grup este în continuare izomorf .
τeud{\ displaystyle \ tau _ {id}}
poate fi legat de sine prin două permutări: identitate și aplicație . Generalizând orice ordine, spațiul poate fi prevăzut cu un grup de automorfisme alcătuite din astfel de mapări. Acest grup este în continuare izomorf .
τeud{\ displaystyle \ tau _ {id}} τ(12){\ displaystyle \ tau _ {(12)}}
τ(12){\ displaystyle \ tau _ {(12)}} E=E⊗k{\ displaystyle {\ mathcal {E}} = E ^ {\ otimes k}}
E=E⊗k{\ displaystyle {\ mathcal {E}} = E ^ {\ otimes k}} Sk{\ displaystyle {\ mathfrak {S}} _ {k}}
Sk{\ displaystyle {\ mathfrak {S}} _ {k}}
Această lipsă de unicitate în cazul general necesită luarea în considerare a ordinii indicilor. De fapt, în general ne abținem să considerăm produsul tensor al spațiilor ca fiind comutativ.
Proprietăți
Transpunere
În cazul unui produs de două spații, harta poate fi numită transpunere . Această noțiune este în concordanță cu cea a transpunerii liniare a aplicației . Știm de fapt că o hartă liniară a lui in poate fi reprezentată de un tensor . Tensorul transpus , elementul de atunci reprezintă harta transpusă , harta in .
τ(12){\ displaystyle \ tau _ {(12)}} f{\ displaystyle f}
f{\ displaystyle f} E{\ displaystyle E}
E{\ displaystyle E} F{\ displaystyle F}
F{\ displaystyle F} T∈F⊗E∗{\ displaystyle T \ in F \ otimes E ^ {*}}
T∈F⊗E∗{\ displaystyle T \ in F \ otimes E ^ {*}} tT=τ(12)T{\ displaystyle {} ^ {t} T = \ tau _ {(12)} T}
tT=τ(12)T{\ displaystyle {} ^ {t} T = \ tau _ {(12)} T} E∗⊗F=E∗⊗(F∗)∗{\ displaystyle E ^ {*} \ otimes F = E ^ {*} \ otimes (F ^ {*}) ^ {*}}
E∗⊗F=E∗⊗(F∗)∗{\ displaystyle E ^ {*} \ otimes F = E ^ {*} \ otimes (F ^ {*}) ^ {*}} tf{\ displaystyle {} ^ {t} f}
tf{\ displaystyle {} ^ {t} f} F∗{\ displaystyle F ^ {*}}
F∗{\ displaystyle F ^ {*}} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}}
 Compoziție și revers
Compoziție și revers
Pentru două permutări și de , avem:
σ{\ displaystyle \ sigma} σ′{\ displaystyle \ sigma '}
σ′{\ displaystyle \ sigma '} Sk{\ displaystyle {\ mathfrak {S}} _ {k}}
Sk{\ displaystyle {\ mathfrak {S}} _ {k}}
τσ∘τσ′=τσ∘σ′{\ displaystyle \ tau _ {\ sigma} \ circ \ tau _ {\ sigma '} = \ tau _ {\ sigma \ circ \ sigma'}} (τσ)-1=τ(σ-1){\ displaystyle \ left (\ tau _ {\ sigma} \ right) ^ {- 1} = \ tau _ {(\ sigma ^ {- 1})}}
(τσ)-1=τ(σ-1){\ displaystyle \ left (\ tau _ {\ sigma} \ right) ^ {- 1} = \ tau _ {(\ sigma ^ {- 1})}}
Algebra tensorială
Definiție
Având în vedere un spațiu vectorial dimensional finit numim tensor pe timpi contravarianți și timpi covarianți (sau tensori ) orice element al . și sunt varianțele acestui tip de tensor, este ordinea (sau rangul ) lor. Tensorii de tip formează un spațiu vectorial. Remediem notațiile:
E{\ displaystyle E} E{\ displaystyle E}
E{\ displaystyle E} k{\ displaystyle k}
k{\ displaystyle k} l{\ displaystyle l}
l{\ displaystyle l} (k,l){\ displaystyle (k, l)}
(k,l){\ displaystyle (k, l)} E⊗k⊗(E∗)⊗l{\ displaystyle E ^ {\ otimes k} \ otimes (E ^ {*}) ^ {\ otimes l}}
E⊗k⊗(E∗)⊗l{\ displaystyle E ^ {\ otimes k} \ otimes (E ^ {*}) ^ {\ otimes l}} k{\ displaystyle k}
k{\ displaystyle k} l{\ displaystyle l}
l{\ displaystyle l} k+l{\ displaystyle k + l}
k+l{\ displaystyle k + l} (k,l){\ displaystyle (k, l)}
(k,l){\ displaystyle (k, l)}
- TlkE=E⊗k⊗(E∗)⊗l{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E = E ^ {\ otimes k} \ otimes (E ^ {*}) ^ {\ otimes l}}

- TkE=T0kE=E⊗k{\ displaystyle {\ mathcal {T}} ^ {k} E = {\ mathcal {T}} _ {0} ^ {k} E = E ^ {\ otimes k}}

- TlE=Tl0E=TlE∗=(E∗)⊗l{\ displaystyle {\ mathcal {T}} _ {l} E = {\ mathcal {T}} _ {l} ^ {0} E = {\ mathcal {T}} ^ {l} E ^ {*} = (E ^ {*}) ^ {\ otimes l}}

Algebra tensorilor notați este definită conform autorilor, fie ca sumă directă a spațiilor tensorilor contravarianți, fie ca sumă directă a spațiilor tensorilor contravarianți și covarianți. Pentru a distinge aceste două cazuri, adoptăm următoarele notații (neconvenționale):
E{\ displaystyle E} TE{\ displaystyle {\ mathcal {T}} E}
TE{\ displaystyle {\ mathcal {T}} E}
- T⋆E=⨁k≥0TkE{\ displaystyle {\ mathcal {T}} ^ {\ star} E = \ bigoplus _ {k \ geq 0} {\ mathcal {T}} ^ {k} E}

- T⋆⋆E=⨁k≥0,l≥0TlkE{\ displaystyle {\ mathcal {T}} _ {\ star} ^ {\ star} E = \ bigoplus _ {k \ geq 0, l \ geq 0} {\ mathcal {T}} _ {l} ^ {k } E}

Algebrele și sunt algebre peste corp . Sunt chiar algebre gradate și respectiv ; ambele de dimensiune infinită.
(T⋆E,K,+,⋅,⊗){\ displaystyle ({\ mathcal {T}} ^ {\ star} E, \ mathbb {K}, +, \ cdot, \ otimes)} (T⋆⋆E,K,+,⋅,⊗){\ displaystyle ({\ mathcal {T}} _ {\ star} ^ {\ star} E, \ mathbb {K}, +, \ cdot, \ otimes)}
(T⋆⋆E,K,+,⋅,⊗){\ displaystyle ({\ mathcal {T}} _ {\ star} ^ {\ star} E, \ mathbb {K}, +, \ cdot, \ otimes)} K{\ displaystyle \ mathbb {K}}
K{\ displaystyle \ mathbb {K}} NU{\ displaystyle \ mathbb {N}}
NU{\ displaystyle \ mathbb {N}} NU2{\ displaystyle \ mathbb {N} ^ {2}}
NU2{\ displaystyle \ mathbb {N} ^ {2}}
Supra remarcat Algebra exterior are legături privilegiate cu algebra din cauza unei posibile injectarea de spații în .
E{\ displaystyle E} ΛE{\ displaystyle \ Lambda E}
ΛE{\ displaystyle \ Lambda E} T⋆E{\ displaystyle {\ mathcal {T}} ^ {\ star} E}
T⋆E{\ displaystyle {\ mathcal {T}} ^ {\ star} E} ΛkE{\ displaystyle \ Lambda ^ {k} E}
ΛkE{\ displaystyle \ Lambda ^ {k} E} TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
Elemente
- Algebra tensorială este definită în principal pentru a da o structură generală setului de tensori. Aceasta necesită extinderea adăugării care nu este definită a priori între elementele și ale lui si . Pentru a face acest lucru, trebuie introduse elemente suplimentare. Astfel, luând în considerare, de exemplu , un element, este formal o secvență astfel încât și, prin definiție, sume directe, dintre care doar un număr finit de elemente este diferit de zero. Cu toate acestea , în fizică și în multe aplicații numai elementele care aparțin subspații de tip sau sunt luate în considerare (acestea sunt singurele pentru care noțiunile de ordine și varianță au o semnificație). Uneori sunt numite elemente omogene ale algebrei gradate .Tl1k1E{\ displaystyle {\ mathcal {T}} _ {l_ {1}} ^ {k_ {1}} E}
 Tl2k2E{\ displaystyle {\ mathcal {T}} _ {l_ {2}} ^ {k_ {2}} E}
Tl2k2E{\ displaystyle {\ mathcal {T}} _ {l_ {2}} ^ {k_ {2}} E} (k1,l1)≠(k2,l2){\ displaystyle (k_ {1}, l_ {1}) \ neq (k_ {2}, l_ {2})}
(k1,l1)≠(k2,l2){\ displaystyle (k_ {1}, l_ {1}) \ neq (k_ {2}, l_ {2})} T⋆E{\ displaystyle {\ mathcal {T}} ^ {\ star} E}
T⋆E{\ displaystyle {\ mathcal {T}} ^ {\ star} E} (T0,T1,T2,⋯){\ displaystyle (T_ {0}, T_ {1}, T_ {2}, \ cdots)}
(T0,T1,T2,⋯){\ displaystyle (T_ {0}, T_ {1}, T_ {2}, \ cdots)} Tk∈TkE{\ displaystyle T_ {k} \ in {\ mathcal {T}} ^ {k} E}
Tk∈TkE{\ displaystyle T_ {k} \ in {\ mathcal {T}} ^ {k} E} TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E}
TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E} TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
- Elementele (cu ) se numesc în general tensori contravarianți , cele ale (cu ) tensori covarianți și cele ale (cu ) tensori mixți .TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
 k>0{\ displaystyle k> 0}
k>0{\ displaystyle k> 0} TlE{\ displaystyle {\ mathcal {T}} _ {l} E}
TlE{\ displaystyle {\ mathcal {T}} _ {l} E} l>0{\ displaystyle l> 0}
l>0{\ displaystyle l> 0} TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E}
TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E} (k,l)>0{\ displaystyle (k, l)> 0}
(k,l)>0{\ displaystyle (k, l)> 0}
- Strict vorbind, algebra nu oferă a priori libertate în ceea ce privește ordinea indicilor covarianți și contravarianți. De exemplu, nu conține spațiu . Cu toate acestea, este în general de acord că un astfel de spațiu este, dacă este necesar, asimilat prin permutarea indicilor (indicii contravarianți sunt deplasați înainte dacă este necesar):T⋆⋆E{\ displaystyle {\ mathcal {T}} _ {\ star} ^ {\ star} E}
 E⊗E∗⊗E⊗E∗⊗E∗{\ displaystyle E \ otimes E ^ {*} \ otimes E \ otimes E ^ {*} \ otimes E ^ {*}}
E⊗E∗⊗E⊗E∗⊗E∗{\ displaystyle E \ otimes E ^ {*} \ otimes E \ otimes E ^ {*} \ otimes E ^ {*}} E⊗E⊗E∗⊗E∗⊗E∗{\ displaystyle E \ otimes E \ otimes E ^ {*} \ otimes E ^ {*} \ otimes E ^ {*}}
E⊗E⊗E∗⊗E∗⊗E∗{\ displaystyle E \ otimes E \ otimes E ^ {*} \ otimes E ^ {*} \ otimes E ^ {*}}
(S⊗T)(ϕ,ψ,tu,v,w)=S(ϕ,tu)⋅T(ψ,v,w){\ displaystyle (S \ otimes T) (\ phi, \ psi, u, v, w) = S (\ phi, u) \ cdot T (\ psi, v, w)}
Această permutare permite afirmarea faptului că produsul tensor este într-adevăr o operație internă .
T⋆⋆E{\ displaystyle {\ mathcal {T}} _ {\ star} ^ {\ star} E}
Proprietăți
Ordin
Dacă și sunt tensori respectiv și pe atunci este (supusă permutarea indicilor) tensorul .
S{\ displaystyle S} T{\ displaystyle T}
T{\ displaystyle T} (k1,l1){\ displaystyle (k_ {1}, l_ {1})}
(k1,l1){\ displaystyle (k_ {1}, l_ {1})} (k2,l2){\ displaystyle (k_ {2}, l_ {2})}
(k2,l2){\ displaystyle (k_ {2}, l_ {2})} E{\ displaystyle E}
E{\ displaystyle E} S⊗T{\ displaystyle S \ otimes T}
S⊗T{\ displaystyle S \ otimes T} (k1+k2,l1+l2){\ displaystyle (k_ {1} + k_ {2}, l_ {1} + l_ {2})}
(k1+k2,l1+l2){\ displaystyle (k_ {1} + k_ {2}, l_ {1} + l_ {2})}
- S⊗T∈Tl1+l2k1+k2E{\ displaystyle S \ otimes T \ in {\ mathcal {T}} _ {l_ {1} + l_ {2}} ^ {k_ {1} + k_ {2}} E}

Un produs contractat (pe indici care trebuie precizați) este un tensor . În general vorbind, orice operațiune de contracție scade covarianța și contravarianța cu 1. Prin urmare, reduce ordinea de 2.
S⊙T{\ displaystyle S \ odot T} (k1+k2-1,l1+l2-1){\ displaystyle (k_ {1} + k_ {2} -1, l_ {1} + l_ {2} -1)}
(k1+k2-1,l1+l2-1){\ displaystyle (k_ {1} + k_ {2} -1, l_ {1} + l_ {2} -1)}
- S⊙T∈Tl1+l2-1k1+k2-1E{\ displaystyle S \ odot T \ in {\ mathcal {T}} _ {l_ {1} + l_ {2} -1} ^ {k_ {1} + k_ {2} -1} E}

Urma endomorfismelor
Un endomorfism al poate fi văzut ca un element , cu alte cuvinte un tensor . Urma acestui endomorfism este valabilă ; adică rezultatul contracției în raport cu cei doi indici ai săi.
E{\ displaystyle E} T∈T11E{\ displaystyle T \ in {\ mathcal {T}} _ {1} ^ {1} E}
T∈T11E{\ displaystyle T \ in {\ mathcal {T}} _ {1} ^ {1} E} (1,1){\ displaystyle (1,1)}
(1,1){\ displaystyle (1,1)} tr(T)=tr12(T){\ displaystyle \ mathrm {tr} (T) = \ mathrm {tr} _ {12} (T)}
tr(T)=tr12(T){\ displaystyle \ mathrm {tr} (T) = \ mathrm {tr} _ {12} (T)} T{\ displaystyle T}
T{\ displaystyle T}
Simetrie și antisimetrie
Fie un tensor de și doi indici și corespunzând aceluiași spațiu vectorial (adică , fie pentru cei doi indici).
T{\ displaystyle T} TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E}
TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E} eu{\ displaystyle i}
eu{\ displaystyle i} j{\ displaystyle j}
j{\ displaystyle j} E{\ displaystyle E}
E{\ displaystyle E} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}}
Spunem că este simetric în raport cu indicii și dacă .
T{\ displaystyle T} eu{\ displaystyle i}
eu{\ displaystyle i} j{\ displaystyle j}
j{\ displaystyle j} τ(euj)T=T{\ displaystyle \ tau _ {(ij)} T = T}
τ(euj)T=T{\ displaystyle \ tau _ {(ij)} T = T}
Spunem că este antisimetric în raport cu indicii și dacă .
T{\ displaystyle T} eu{\ displaystyle i}
eu{\ displaystyle i} j{\ displaystyle j}
j{\ displaystyle j} τ(euj)T=-T{\ displaystyle \ tau _ {(ij)} T = -T}
τ(euj)T=-T{\ displaystyle \ tau _ {(ij)} T = -T}
Spunem că este total simetric dacă este simetric pentru orice pereche de indici. Prin urmare, este necesar ca acesta să aparțină sau .
T{\ displaystyle T} TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
TkE{\ displaystyle {\ mathcal {T}} ^ {k} E} TlE{\ displaystyle {\ mathcal {T}} _ {l} E}
TlE{\ displaystyle {\ mathcal {T}} _ {l} E}
Spunem că este total antisimetric dacă este antisimetric pentru orice pereche de indici. Din nou, spațiul trebuie să fie sau .
T{\ displaystyle T} TkE{\ displaystyle {\ mathcal {T}} ^ {k} E}
TkE{\ displaystyle {\ mathcal {T}} ^ {k} E} TlE{\ displaystyle {\ mathcal {T}} _ {l} E}
TlE{\ displaystyle {\ mathcal {T}} _ {l} E}
Produs scalar
Un produs scalar real pe un spațiu dimensional finit este un caz particular al unui tensor simetric pe care îl putem nota . De asemenea, este definit și pozitiv. Deci avem :(⋅|⋅){\ displaystyle (\ cdot | \ cdot)} E{\ displaystyle E}
E{\ displaystyle E} R{\ displaystyle \ mathbb {R}}
R{\ displaystyle \ mathbb {R}} (0,2){\ displaystyle (0,2)}
(0,2){\ displaystyle (0,2)} g{\ displaystyle g}
g{\ displaystyle g}
(tu|v)=g(tu,v)=tu⊙g⊙v{\ displaystyle (u | v) = g (u, v) = u \ odot g \ odot v}
Cazul spațiilor euclidiene și pătratice
Într-un spațiu euclidian (sau mai general într-un spațiu pătratic non-degenerat) , existența unui produs scalar real (respectiv a unui produs pseudo-scalar, adică a unei forme biliniare nesimetrice degenerează sau echivalent o formă pătratică non-degenerată ) oferă proprietăți specifice tensoarelor. Acest lucru face posibilă stabilirea unui izomorfism canonic care să asocieze o singură formă liniară cu orice vector:
E{\ displaystyle E} g{\ displaystyle g}
g{\ displaystyle g} mg:tu∈E↦(g⊙tu)∈E∗{\ displaystyle m_ {g}: u \ in E \ mapsto (g \ odot u) \ in E ^ {*}}
mg:tu∈E↦(g⊙tu)∈E∗{\ displaystyle m_ {g}: u \ in E \ mapsto (g \ odot u) \ in E ^ {*}}
Produsul (pseudo-) dot pe de asemenea definește în mod natural un produs (pseudo-) dot pe . Acesta este elementul unic , putem nota , de verificare pentru orice , și toate , . Izomorfismul are pentru reciprocitate .
E{\ displaystyle E} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}} E⊗E{\ displaystyle E \ otimes E}
E⊗E{\ displaystyle E \ otimes E} g∗{\ displaystyle g ^ {*}}
g∗{\ displaystyle g ^ {*}} tu∈E{\ displaystyle u \ in E}
tu∈E{\ displaystyle u \ in E} g∗⊙g⊙tu=tu⊙g⊙g∗=tu{\ displaystyle g ^ {*} \ odot g \ odot u = u \ odot g \ odot g ^ {*} = u}
g∗⊙g⊙tu=tu⊙g⊙g∗=tu{\ displaystyle g ^ {*} \ odot g \ odot u = u \ odot g \ odot g ^ {*} = u} ϕ∈E∗{\ displaystyle \ phi \ în E ^ {*}}
ϕ∈E∗{\ displaystyle \ phi \ în E ^ {*}} g⊙g∗⊙ϕ=ϕ⊙g∗⊙g=ϕ{\ displaystyle g \ odot g ^ {*} \ odot \ phi = \ phi \ odot g ^ {*} \ odot g = \ phi}
g⊙g∗⊙ϕ=ϕ⊙g∗⊙g=ϕ{\ displaystyle g \ odot g ^ {*} \ odot \ phi = \ phi \ odot g ^ {*} \ odot g = \ phi} mg{\ displaystyle m_ {g}}
mg{\ displaystyle m_ {g}} mg-1:ϕ∈E∗↦(g∗⊙ϕ)∈E{\ displaystyle m_ {g} ^ {- 1}: \ phi \ în E ^ {*} \ mapsto (g ^ {*} \ odot \ phi) \ în E}
mg-1:ϕ∈E∗↦(g∗⊙ϕ)∈E{\ displaystyle m_ {g} ^ {- 1}: \ phi \ în E ^ {*} \ mapsto (g ^ {*} \ odot \ phi) \ în E}
Asimilarea cu dualul
Prin izomorfismul poate apoi absorbi orice componentă a unui element : . În general, acest lucru face posibil să nu se mai facă distincția între indicii contravarianți și indici covarianți . În aceste condiții, un tensor de tip poate fi văzută ca un tensor precum și . Ordinea devine apoi o caracteristică suficientă pentru a clasifica orice tensor construit .
mg{\ displaystyle m_ {g}} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}} E{\ displaystyle E}
E{\ displaystyle E} mg(tu)≈tu{\ displaystyle m_ {g} (u) \ approx u}
mg(tu)≈tu{\ displaystyle m_ {g} (u) \ approx u} (k,l){\ displaystyle (k, l)}
(k,l){\ displaystyle (k, l)} (k+l,0){\ displaystyle (k + l, 0)}
(k+l,0){\ displaystyle (k + l, 0)} (0,k+l){\ displaystyle (0, k + l)}
(0,k+l){\ displaystyle (0, k + l)} k+l{\ displaystyle k + l}
k+l{\ displaystyle k + l} E{\ displaystyle E}
E{\ displaystyle E}
Proprietăți
Corespondența dintre produsele scalare și contractate
Devine posibilă contractarea a doi vectori ai . Această contracție este identificată cu produsul scalar:E{\ displaystyle E} tu⊙v=(tu|v){\ displaystyle u \ odot v = (u | v)}
tu⊙v=(tu|v){\ displaystyle u \ odot v = (u | v)}
 Contracții pe orice indice
Contracții pe orice indice
Acum putem contracta doi indici care corespund aceluiași spațiu pătratic prin utilizarea implicită a produsului scalar:
E{\ displaystyle E}
 Despre spațiile hermitiene
Despre spațiile hermitiene
Un produs scalar hermitian nu este un tensor: este într-adevăr doar semiliniar în raport cu prima sa variabilă. De fapt, proprietățile menționate mai sus nu se aplică în contextul spațiilor hermitiene .
Calcul convenabil
Manipularea eficientă a tensorilor necesită, în general, reprezentarea lor în baze particulare (dar totuși arbitrare). Să fie o bază de . Vom remarca baza sa duală. Apoi orice tensor de poate fi scris ca o combinație liniară de tipul:
Dacă baza este specificată în avans, datele scalare caracterizează pe deplin tensorul. Ele reprezintă coordonatele tensorului în baza luată în considerare. Setul de convenții pentru utilizarea coordonatelor tensoarelor se numește convenția Einstein . Este posibil să se amestece indici covarianți și contravarianți. Indicii contrarianți sunt notați cu indici mai mari, indicii covarianți cu indici mai mici. Astfel se descompune într-o bază dată cu componentele .
(e1,e2,⋯,enu){\ displaystyle (e_ {1}, e_ {2}, \ cdots, e_ {n})} E{\ displaystyle E}
E{\ displaystyle E} (e1,e2,...enu){\ displaystyle (e ^ {1}, e ^ {2}, ... e ^ {n})}
(e1,e2,...enu){\ displaystyle (e ^ {1}, e ^ {2}, ... e ^ {n})} T{\ displaystyle T}
T{\ displaystyle T} TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E}
TlkE{\ displaystyle {\ mathcal {T}} _ {l} ^ {k} E} T=∑eu1,⋯,euk∑j1,⋯,jlTeu1⋯eukj1⋯jl⋅eeu1⊗⋯⊗eeuk⊗ej1⊗⋯⊗ejl{\ displaystyle T = \ sum _ {i_ {1}, \ cdots, i_ {k}} \ sum _ {j_ {1}, \ cdots, j_ {l}} T ^ {i_ {1} \ cdots i_ { k}} {} _ {j_ {1} \ cdots j_ {l}} \ cdot e_ {i_ {1}} \ otimes \ cdots \ otimes e_ {i_ {k}} \ otimes e ^ {j_ {1}} \ otimes \ cdots \ otimes e ^ {j_ {l}}}
T=∑eu1,⋯,euk∑j1,⋯,jlTeu1⋯eukj1⋯jl⋅eeu1⊗⋯⊗eeuk⊗ej1⊗⋯⊗ejl{\ displaystyle T = \ sum _ {i_ {1}, \ cdots, i_ {k}} \ sum _ {j_ {1}, \ cdots, j_ {l}} T ^ {i_ {1} \ cdots i_ { k}} {} _ {j_ {1} \ cdots j_ {l}} \ cdot e_ {i_ {1}} \ otimes \ cdots \ otimes e_ {i_ {k}} \ otimes e ^ {j_ {1}} \ otimes \ cdots \ otimes e ^ {j_ {l}}} Teu1⋯eukj1⋯jl{\ displaystyle T ^ {i_ {1} \ cdots i_ {k}} {} _ {j_ {1} \ cdots j_ {l}}}
Teu1⋯eukj1⋯jl{\ displaystyle T ^ {i_ {1} \ cdots i_ {k}} {} _ {j_ {1} \ cdots j_ {l}}} T{\ displaystyle T}
T{\ displaystyle T} Δ∈E∗⊗E∗⊗E⊗E∗⊗E∗⊗E{\ displaystyle \ Delta \ in E ^ {*} \ otimes E ^ {*} \ otimes E \ otimes E ^ {*} \ otimes E ^ {*} \ otimes E}
Δ∈E∗⊗E∗⊗E⊗E∗⊗E∗⊗E{\ displaystyle \ Delta \ in E ^ {*} \ otimes E ^ {*} \ otimes E \ otimes E ^ {*} \ otimes E ^ {*} \ otimes E} Δeujklmnu{\ displaystyle \ Delta _ {ij} {} ^ {k} {} _ {lm} {} ^ {n}}
Δeujklmnu{\ displaystyle \ Delta _ {ij} {} ^ {k} {} _ {lm} {} ^ {n}}
Cu toate acestea, este posibilă interpretarea aceleiași notații folosind indici cu o semnificație intrinsecă (adică fără apelarea la coordonate). Acesta este apoi ratingul abstract al indexului .
Legături între evaluări
Ne oferim următoarele tensori:
- Scalari: λ∈K,μ∈K,ν∈K{\ displaystyle \ lambda \ in \ mathbb {K}, \ mu \ in \ mathbb {K}, \ nu \ in \ mathbb {K}}

- Vectori: tu∈E,v∈E,w∈E{\ displaystyle u \ in E, v \ in E, w \ in E}

- Covectori (forme liniare): ϕ∈E∗,ψ∈E∗,χ∈E∗{\ displaystyle \ phi \ in E ^ {*}, \ psi \ in E ^ {*}, \ chi \ in E ^ {*}}

- Tensori de ordinul 2:
- T∈E∗⊗E{\ displaystyle T \ in E ^ {*} \ otimes E}

- S∈E∗⊗E∗{\ displaystyle S \ in E ^ {*} \ otimes E ^ {*}}

- R∈E⊗E∗{\ displaystyle R \ in E \ otimes E ^ {*}}

- Î∈E∗⊗E∗{\ displaystyle Q \ in E ^ {*} \ otimes E ^ {*}}

- P∈E⊗E{\ displaystyle P \ in E \ otimes E}

- O∈E⊗E∗{\ displaystyle O \ in E \ otimes E ^ {*}}

- Tensori de ordinul 3 și mai mult:
- Ω∈E∗⊗E∗⊗E{\ displaystyle \ Omega \ in E ^ {*} \ otimes E ^ {*} \ otimes E}

- Φ∈E⊗E⊗E∗{\ displaystyle \ Phi \ in E \ otimes E \ otimes E ^ {*}}

- Δ∈E∗⊗E∗⊗E⊗E∗⊗E∗⊗E{\ displaystyle \ Delta \ in E ^ {*} \ otimes E ^ {*} \ otimes E \ otimes E ^ {*} \ otimes E ^ {*} \ otimes E}

- Γ∈E⊗E∗⊗E∗⊗E⊗E∗⊗E∗{\ displaystyle \ Gamma \ in E \ otimes E ^ {*} \ otimes E ^ {*} \ otimes E \ otimes E ^ {*} \ otimes E ^ {*}}

De asemenea, alegem o bază în . Această alegere o induce în mod natural pe cea a bazei duale în . Tensorii definiți anterior admit apoi o singură descompunere în aceste baze.
(e1,e2,⋯){\ displaystyle (e_ {1}, e_ {2}, \ cdots)} E{\ displaystyle E}
E{\ displaystyle E} (e1,e2,⋯){\ displaystyle (e ^ {1}, e ^ {2}, \ cdots)}
(e1,e2,⋯){\ displaystyle (e ^ {1}, e ^ {2}, \ cdots)} E∗{\ displaystyle E ^ {*}}
E∗{\ displaystyle E ^ {*}}
Notarea operațiilor în spații dimensionale finite
| Proprietăți
|
Evaluare fără indici
|
Convenția Einstein / notația indexului abstract
|
|---|
| Produs tensor
|
T=ϕ⊗tu{\ displaystyle T = \ phi \ otimes u}
|
Teuj=ϕeutuj{\ displaystyle T_ {i} {} ^ {j} = \ phi _ {i} \; u ^ {j}}
|
Δ=S⊗v⊗Ω{\ displaystyle \ Delta = S \ otimes v \ otimes \ Omega}
|
Δeujklmnu=SeujvkΩlmnu{\ displaystyle \ Delta _ {ij} {} ^ {k} {} _ {lm} {} ^ {n} = S_ {ij} \; v ^ {k} \; \ Omega _ {lm} {} ^ {nu}}
|
R+v⊗χ=O{\ displaystyle R + \ otimes \ chi = O}
|
Reuj+veuχj=Oeuj{\ displaystyle R ^ {i} {} _ {j} + v ^ {i} \; \ chi _ {j} = O ^ {i} {} _ {j}}
|
| Produs contractat
|
λ=ϕ⊙tu=ϕ⊗¯tu{\ displaystyle \ lambda = \ phi \ odot u = \ phi \; {\ bar {\ otimes}} \; u}
|
λ=ϕmtum{\ displaystyle \ lambda = \ phi _ {m} \; u ^ {m}}
|
v⊙Ω⊙ϕ=λ⋅S⊙P⊙χ+ψ{\ displaystyle v \ odot \ Omega \ odot \ phi = \ lambda \ cdot S \ odot P \ odot \ chi + \ psi}
|
vmΩmeunuϕnu=λSeupPpqχq+ψeu{\ displaystyle v ^ {m} \; \ Omega _ {mi} {} ^ {n} \; \ phi _ {n} = \ lambda \; S_ {ip} \; P ^ {pq} \; \ chi _ {q} + \ psi _ {i}}
|
| Contracție
|
μ=tr12(T){\ displaystyle \ mu = \ mathrm {tr} _ {12} (T)}
|
μ=Tmm{\ displaystyle \ mu = T_ {m} {} ^ {m}}
|
tr13(Φ)=w{\ displaystyle \ mathrm {tr} _ {13} (\ Phi) = w}
|
Φmeum=weu{\ displaystyle \ Phi ^ {mi} {} _ {m} = w ^ {i}}
|
| Permutarea indicilor
|
T=τ(12)(R)=tR{\ displaystyle T = \ tau _ {(12)} (R) = {} ^ {t} R}
|
Teuj=Rjeu{\ displaystyle T_ {i} {\;} ^ {j} = R ^ {j} {} _ {i}}
|
Γ=τ(123)(46)(Δ){\ displaystyle \ Gamma = \ tau _ {(123) (46)} (\ Delta)}
|
Γeujklmnu=Δjkeunuml{\ displaystyle \ Gamma ^ {i} {} _ {jk} {} ^ {l} {} _ {mn} = \ Delta _ {jk} {} ^ {i} {} _ {nm} {} ^ { l}}
|
| Amestecat
|
tr26(Δ)⊗¯¯Φ+τ(23)(Ω)=χ⊗P⊙Î{\ displaystyle \ mathrm {tr} _ {26} (\ Delta) \; {\ bar {\ bar {\ otimes}}} \; \ Phi + \ tau _ {(23)} (\ Omega) = \ chi \ otimes P \ odot Q}
|
ΔeumjnupmΦpnuk+Ωeukj=χeuPjqÎqk{\ displaystyle \ Delta _ {im} {} ^ {j} {} _ {np} {} ^ {m} \; \ Phi ^ {pn} {} _ {k} + \ Omega _ {ik} {} ^ {j} = \ chi _ {i} \; P ^ {jq} \; Q_ {qk}}
|
Legături între notații în cazul spațiilor pătratice
De asemenea, luăm în considerare existența produsului (pseudo-) scalar .
g∈E∗⊗E∗{\ displaystyle g \ in E ^ {*} \ otimes E ^ {*}}
Notarea operațiilor în spațiile euclidiene
| Proprietăți
|
Evaluare fără indici
|
Convenția Einstein / notația indexului abstract
|
|---|
| Produs contractat
|
ν=tu⊙v{\ displaystyle \ nu = u \ odot v}
|
ν=tumgmnuvnu{\ displaystyle \ nu = u ^ {m} \; g_ {mn} \; v ^ {n}}
|
tu=P⊙w{\ displaystyle u = P \ odot w}
|
tueu=Peumgmnuwnu{\ displaystyle u ^ {i} = P ^ {im} \; g_ {mn} \; w ^ {n}}
|
| Contracție
|
ϕ=tr12(Φ){\ displaystyle \ phi = \ mathrm {tr} _ {12} (\ Phi)}
|
ϕeu=gmnuΦnumeu{\ displaystyle \ phi _ {i} = g_ {mn} \; \ Phi ^ {nm} {} _ {i}}
|
Despre schimbări de bază
Rețineți că numai convenția lui Einstein admite formule de schimbare a bazei. Într-adevăr, întrucât este nevoie de partid pentru a reprezenta un tensor printr-un set de coordonate într-o bază predefinită (sau chiar mai multe baze), există formule pentru a determina coordonatele aceluiași tensor într-o bază nouă (cum ar fi ). Notările fără indici și în indici abstracte fiind, prin definiție, independente de o alegere de bază, nu admit echivalenți pentru aceste formule.
Ω^lmnu=αleuαmjβnukΩeujk{\ displaystyle {\ hat {\ Omega}} _ {lm} {} ^ {n} = \ alpha _ {l} {} ^ {i} \; \ alpha _ {m} {} ^ {j} \; \ beta ^ {n} {} _ {k} \; \ Omega _ {ij} {} ^ {k}}
Referințe
-
deoarece cele 2 spații vectoriale și sunt de dimensiune finităE{\ displaystyle E}
 F{\ displaystyle F}
F{\ displaystyle F}
Anexe
Articole similare
linkuri externe
Bibliografie
- Laurent Schwartz , Les tenseurs , Hermann,1975( ISBN 2-7056-1376-5 )
-
Roger Godement , Cours d'Algèbre , Paris, Hermann, 1966, §21 și în special p. 268-269.
- Roger Godement, Analiza matematică III. Funcții analitice, diferențiale și multiple , suprafețe Riemann , Springer, 2001; capitolul IX, p. 139-174 (cu divagările sale istorice și batjocoritoare).
-
Mikhail Postnikov , lecții de geometrie: II - lea semestru: Algebra liniara si geometrie diferentiala , Moscova, Editions Mir , 1981
<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">

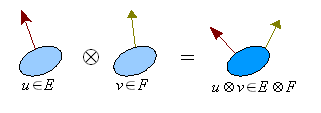
 Non-comutativitate
Non-comutativitate
 Distributivitate
Distributivitate
 Bazele domeniilor de produse
Bazele domeniilor de produse



 Imagine prin aplicație liniară
Imagine prin aplicație liniară

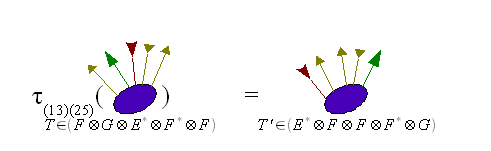
 Compoziție și revers
Compoziție și revers

 Contracții pe orice indice
Contracții pe orice indice
 Despre spațiile hermitiene
Despre spațiile hermitiene









































































































































![\ forall u \ in E ^ {*}, \ forall v \ in F ^ {*}, \ quad \ left [\ tau _ {{(12)}} T \ right] (v, u) = T (u , v)](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d9f7d9c4b082516dd90b4943ea2bc896cec8ce4)




![\ forall v_ {i} \ în E_ {i} ^ {*}, \ quad \ left [\ tau _ {\ sigma} T \ right] (v _ {{\ sigma (1)}}, \ cdots, v_ {{\ sigma (k)}}) = T (v_ {1}, \ cdots, v_ {k})](https://wikimedia.org/api/rest_v1/media/math/render/svg/679dec6d2519ffcad4063b85982329f207814922)































































































































