Teorema restului chinezesc

În matematică , teorema restului chinez este un rezultat al aritmeticii modulare care se ocupă cu rezoluția sistemelor de congruență . Acest rezultat, stabilit inițial pentru ℤ / nℤ , se generalizează în teoria inelului . Această teoremă este utilizată în teoria numerelor .

Fragmente de istorie

Exemplu de Sun Zi

Forma originală a teoremei apare ca o problemă în cartea lui Sun Tzu , Sunzi suanjing (în) , datând din secolul al III- lea . Este preluat de matematicianul chinez Qin Jiushao în lucrarea sa Shùshū Jiǔzhāng („ Tratat matematic în nouă capitole ”) publicat în 1247 . Rezultatul se referă la sistemele de congruență (a se vedea aritmetica modulară ).

Fie obiecte de număr necunoscut. Dacă le comandăm cu 3, mai sunt 2. Dacă le comandăm cu 5, mai sunt 3 și dacă sunt sortate după 7, mai sunt 2 . Câte obiecte avem?

Această enigmă este uneori asociată cu generalul Han Xin (ro) numărându-și armata.

Rezoluția propusă de Sun Zi pentru această problemă este următoarea:

Înmulțiți restul diviziunii cu 3, adică 2, cu 70, adăugați produsul restului diviziunii cu 5, adică 3, cu 21, apoi adăugați produsul restului diviziunii cu 7, adică 2 cu 15. Atâta timp cât numărul este mai mare de 105, scade 105.

Dar soluția explică doar în mod imperfect metoda utilizată. Cu toate acestea, putem observa că:

70 are restul 1 în diviziuni cu 3 și restul 0 în divizii cu 5 și 7;
21 are restul 1 în divizii cu 5 și restul 0 în divizii cu 3 și 7;
15 are un rest de 1 în diviziune cu 7 și un rest de 0 în diviziuni cu 3 și 5.

Numărul 2 × 70 + 3 × 21 + 2 × 15 are apoi pentru resturile respective 2, 3 și 2 din diviziunile cu 3, 5 și 7. În cele din urmă, așa cum 105 are pentru restul 0 în cele trei tipuri de diviziune, putem scoateți-l sau adăugați-l de câte ori doriți fără a modifica valorile resturilor. Cea mai mică valoare pentru numărul de obiecte este atunci 23.

Această problemă o găsim aproape identică în 1202 în Abbaci Liber din Fibonacci în capitolul XII cu privire la problemele și puzzle-urile, care este și problema iepurilor din secvența Fibonacci . Problema fusese studiată și de Ibn al-Haytham (Alhazen) - vezi articolul Matematica arabă - ale cărei lucrări le-a putut citi Fibonacci.

Euler a fost, de asemenea, interesat de această întrebare, precum și de Gauss .

Astronomie

Potrivit lui Ulrich Libbrecht (de) , motivația pentru acest tip de calcul în rândul chinezilor este astronomia . Putem într-adevăr să credem că chinezii, dornici de calcule astronomice, ar putea fi interesați de concordanțele calendaristice și că au fost conduși foarte devreme să fie interesați de întrebări de acest tip:

În câte zile va cădea luna plină pe solstițiul de iarnă?

Dacă întrebarea apare când mai sunt 6 zile înainte de solstițiul de iarnă și cu 3 zile înainte de luna plină, întrebarea are ca rezultat:

Există un număr întreg x astfel încât restul din împărțirea x la 365 să fie 6 și restul din împărțirea x la 28 să fie 3?

Numărarea pachetelor

Dar, conform lui Daumas și colab., Este mai probabil să fie probleme asociate cu numărul de pachete, posibil de origine divinatorie.

În cele din urmă, ar fi păcat să nu prezentăm această problemă referitoare la pirați și o comoară, foarte frecvent citată pentru a ilustra teorema restului chinez:

O bandă de 17 pirați are o comoară formată din monede de aur de aceeași valoare. Ei intenționează să le împărtășească în mod egal și să dea restul bucătarului chinez. Aceasta ar primi apoi 3 monede. Dar pirații se ceartă și șase dintre ei sunt uciși. O nouă cotă ar da bucătarului 4 bucăți. Într-un naufragiu ulterior, doar tezaurul, șase pirați și bucătarul sunt salvați, iar partajarea ar da apoi celor din urmă 5 aur. Care este averea minimă la care poate spera bucătarul dacă decide să otrăvească restul piraților?

Răspunsul este 785. Numerele 17, 11 și 6 fiind prime între ele două câte două, soluțiile sunt separate de un multiplu de 1122 (17 × 11 × 6); mai mult, 785 satisface afirmația: 785 = 17 × 46 + 3 = 11 × 71 + 4 = 6 × 130 + 5. Rezultă că 785 este într-adevăr cel mai mic dintre numerele posibile.

Modular aritmetic a făcut această problemă mai ușor de rezolvat.

Sistem de congruență întregi

Teorema

Fie ,…, numere întregi două sau două care sunt primele una față de alta , adică GCD ( n i , n j ) = 1 când i ≠ j . Apoi , pentru toate numere întregi , ... ,, există un întreg , unic modulo , astfel încât $n_1$ $n_k$ $a_1$ $a_ {k}$ $X$ $n = \ prod _ {{i = 1}} ^ {k} n_ {i}$

{\ displaystyle {\ begin {matrix} x \ equiv a_ {1} {\ pmod {n_ {1}}} \\\ ldots \\ x \ equiv a_ {k} {\ pmod {n_ {k}}} \ \\ end {matrix}}}

Algoritm

O soluție poate fi găsită după cum urmează. Pentru fiecare i , numerele întregi și sunt coprimă. Conform teoremei Bachet-Bézout putem calcula inversul lui modulo . Pentru aceasta, putem folosi algoritmul euclidian extins și să obținem numere întregi și astfel încât . Dacă pozăm , atunci avem $X$ $sau$ ${\ hat {n}} _ {i} = {\ frac n {n_ {i}}} = n_ {1} \ ldots n _ {{i-1}} n _ {{i + 1}} \ ldots n_ {k}$ $v_ {i} \,$ ${\ hat n} _ {i}$ $sau$ $u_ {i} \,$ $v_ {i} \,$ $u_ {i} n_ {i} + v_ {i} {\ hat n} _ {i} = 1$ $e_ {i} = v_ {i} {\ hat n} _ {i}$

{\ displaystyle e_ {i} \ equiv 1 {\ pmod {n_ {i}}} \,}

iar pentru j ≠ i .

{\ displaystyle e_ {i} \ equiv 0 {\ pmod {n_ {j}}} \,}

Prin urmare, o soluție specială a acestui sistem de congruență este

x = \ sum _ {{i = 1}} ^ {k} a_ {i} e_ {i} ~,

iar celelalte soluții sunt numerele întregi congruente pentru a modula produsul . $X$ $nu$

Exemplu

Exemplul lui Sun Zi, prezentat mai devreme în secțiunea de istorie, se rezumă la

x \ equiv 2 {\ pmod {3}} \,

x \ equiv 3 {\ pmod {5}} \,

x \ equiv 2 {\ pmod {7}} \,

ajungem atunci

${\ displaystyle n = 3 \ ori 5 \ ori 7 = 105}$
${n_ {1}} = 3$ și , cam așa ${\ hat n} _ {1} = 35$ $2 {\ hat n} _ {1} \ equiv 1 {\ pmod {3}}$ $e_ {1} = 70$
$n_ {2} = 5$ și , cam așa ${\ hat n} _ {2} = 21$ ${\ hat n} _ {2} \ equiv 1 {\ pmod {5}}$ $e_ {2} = 21$
$n_ {3} = 7$ și , cam așa ${\ hat n} _ {3} = 15$ ${\ hat n} _ {3} \ equiv 1 {\ pmod {7}}$ $e_ {3} = 15$

o soluție pentru x este atunci $x = 2 \ ori 70 + 3 \ ori 21 + 2 \ ori 15 = 233$

iar soluțiile sunt toate numere întregi congruente cu 233 modulo 105, adică cu 23 modulo 105.

Generalizare la numere non prime

Sistemele de congruență pot fi rezolvate chiar dacă n i nu sunt prime între ele două câte două. Criteriul precis este următorul:

o soluție x există dacă și numai dacă pentru toate i și j . Setul de soluții x formează apoi o clasă de congruență modul PPCM de n i . $a_ {i} \ equiv a_ {j} {\ pmod {{{\ rm {PGCD}}} (n_ {i}, n_ {j})}}$

Exemplu: sistemul x ≡ –1 mod 4 și x ≡ –1 mod 6 este echivalent cu: x + 1 multiplu de 4 și 6, adică de PPCM (4, 6) = 12, sau din nou: x ≡ - 1 mod 12.

O metodă de rezolvare a acestor sisteme este metoda chineză , care constă în reducerea la module prime între ele două câte două (în exemplul de mai sus: modulele 4 și 3). O alta este metoda substituțiilor succesive .

Interpretare mecanică

Soluția sistemului  , necunoscută , trece prin calculul PPCM al și . $\ left \ {{\ begin {array} {l} x \ equiv r {\ pmod a} \\ x \ equiv s {\ pmod b} \ end {array}} \ right.$ $X$ $la$ $b$

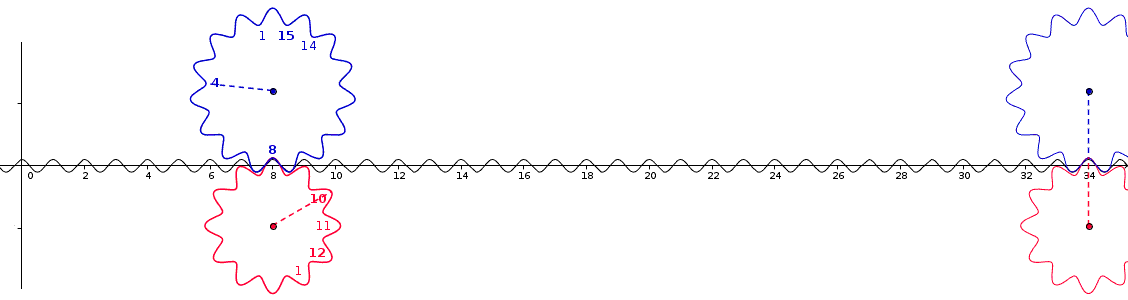
O roată dințată care cuprinde ochiuri dentare cu o altă roată dințată care cuprinde dinții săi . Câți dinți trebuie să treacă pentru ca al doilea dinte să coincidă cu al doilea dinte? $la$ $b$ $r$ $s$

PPCM al celor două numere și este ceea ce face posibilă înțelegerea comportamentului periodic al acestui sistem: este numărul de dinți care separă doi contacte de aceeași congruență. Prin urmare, putem găsi soluția, dacă există, între timp . Există o soluție dacă GCD ( a , b ) împarte r - s . $la$ $b$ $[1, {\ rm {{PPCM} (a, b)]}}$

Pentru acest angrenaj , PPCM (12,15) = 60, pentru x ∈ [1,60], soluția este x = 34. ${\ displaystyle \ left \ {{\ begin {array} {l} x \ equiv 4 ~ (mod ~ 15) \\ x \ equiv 10 ~ (mod ~ 12) \ end {array}} \ right.}$

Putem înțelege cu ușurință de ce calculul pe roțile dințate implică aritmetică modulară, observând că setul dinților unei roți prin numărarea n poate fi parametrizat de setul de n - rădăcini ale unității , care are o structură de grup care este naturală izomorfă cu cea a lui ℤ / n ℤ .

Rezultat pentru inele

În inele Z / n Z

Teorema chineză are , de asemenea , o versiune mai abstractă: dacă $n - 1$ , ..., $n k$ sunt de două până la două numere prime între ele , apoi, prin ceea ce denotă $n$ PPCM a $n i$ , adică în cazul de față produsul de $n i$ , harta (cu valori în inelul de produs )

${\ begin {matrix} \ phi: & \ mathbb {Z} / n \ mathbb {Z} & \ longrightarrow & \ mathbb {Z} / n_ {1} \ mathbb {Z} \ times \ cdots \ times \ mathbb { Z} / n_ {k} \ mathbb {Z} \\ & \ alpha [n] & \ longmapsto & (\ alpha [n_ {1}], \ dots, \ alpha [n_ {k}]) \ end {matrix }}$

este un izomorfism al inelelor .

De exemplu, următorul tabel compară și și fiecare pereche de elemente ale apare exact o dată și o singură dată: ${\ displaystyle \ mathbb {Z} / 15 \ mathbb {Z}}$ ${\ displaystyle \ mathbb {Z} / 3 \ mathbb {Z} \ times \ mathbb {Z} / 5 \ mathbb {Z}}$ ${\ displaystyle \ mathbb {Z} / 3 \ mathbb {Z} \ times \ mathbb {Z} / 5 \ mathbb {Z}}$

X	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
x mod 3	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2
x mod 5	0	1	2	3	4	0	1	2	3	4	0	1	2	3	4

Pentru a arăta acest lucru, observăm mai întâi că cele două seturi și au același număr de elemente. Așa cum este un morfism inelar , este suficient să se demonstreze că este injectiv pentru a deduce că este un izomorfism. Pentru aceasta, este suficient să arate că nucleul său este redus la 0: if for , adică dacă este multiplu al fiecărui $n$ $i$ , atunci , adică este multiplu al produsului $n$ $1$ , ..., $N$ $k$ . Acest lucru rezultă din presupunerea că $n$ $i$ sunt primi între ei doi câte doi. $\ Z / n \ Z$ $\ mathbb {Z} / n_ {1} \ mathbb {Z} \ times \ cdots \ times \ mathbb {Z} / n_ {k} \ mathbb {Z}$ $\ phi$ ${\ displaystyle \ alpha \ equiv 0 \ mod {n_ {i}}}$ $i = 1, \ dots, k$ $\alfa$ ${\ displaystyle \ alpha \ equiv 0 \ mod n}$ $\alfa$

În cazul în care $n i$ nu sunt doi sau doi primii între ei , morfismul de mai sus este doar injectiv. Există o soluție la problema inițială dacă și numai dacă datele sunt în imagine, adică mcd de $n i$ și $n j$ împarte $a i - a j$ pentru orice pereche $( i , j )$ .

Într-un inel principal

Pentru un inel principal R , teorema restului chinezesc ia următoarea formă: Dacă r 1 , ..., r k sunt elemente ale lui R care sunt primele două câte două, iar r denotă produsul r 1 ... r k , atunci morfismul inelelor

${\ begin {matrix} f: & R / rR & \ longrightarrow & R / r_ {1} R \ times \ cdots \ times R / r_ {k} R \\ & x \; {\ mathrm {mod}} \ , rR & \ longmapsto & (x \; {\ mathrm {mod}} \, r_ {1} R, \ cdots, x \; {\ mathrm {mod}} \, r_ {k} R) \ end {matrix }}$

este un izomorfism.

Izomorfismul invers poate fi construit astfel. Pentru fiecare i , elementele r i și r / r i sunt coprimă și, prin urmare, există elemente u i și v i în R astfel încât

u_ {i} r_ {i} + v_ {i} {\ frac rr} _ {i} = 1

Fie e i = v i r / r i . Avem :

e_ {i} \ equiv 1 {\ pmod {r_ {i}}} \ quad {\ mathrm {et}} \ quad e_ {i} \ equiv 0 {\ pmod {r_ {j}}}

pentru j ≠ i .

Apoi inversul lui $f$ este morfismul construit folosind idempotenții e i (mod r ):

${\ begin {matrix} g: & R / r_ {1} R \ times \ cdots \ times R / r_ {k} R & \ longrightarrow & R / rR \\ & (a_ {1} \; {\ mathrm { mod}} \, r_ {1} R, \ cdots, a_ {k} \; {\ mathrm {mod}} \, r_ {k} R) & \ longmapsto & \ sum _ {{i = 1}} ^ {k} a_ {i} e_ {i} \; {\ mathrm {mod}} \, rR ~. \ end {matrix}}$

Exemplu de polinoame

Teorema remanierului chinez ne permite să rezolvăm în mod explicit orice sistem de congruență din inelul euclidian R = K [ X ] al polinoamelor pe un câmp K , adică orice sistem al formei.

$\ forall i \ in \ {0, \ ldots, n \}, P \ equiv A_ {i} {\ pmod {R_ {i}}}$

în cazul în care datele sunt polinoame R i primii doi doi împreună și polinoamele A i și necunoscut este polinomul P .

Lagrangianul corespunde interpolare în cazul particular în care R i sunt de forma X - x i și A i sunt constante , și oferă soluția P de grad ≤ n . Mai explicit, dacă x 0 , x 1 , ..., x n sunt n + 1 elemente de K distincte două câte două, vom lua pentru E i la interpolate polinoame Lagrange , definite prin: $E_ {i} = {(X-x_ {0}) (X-x_ {1}) ... (X-x _ {{i-1}}) (X-x _ {{i + 1}}). .. (X-x_ {n}) \ over (x_ {i} -x_ {0}) (x_ {i} -x_ {1}) ... (x_ {i} -x _ {{i-1}} ) (x_ {i} -x _ {{i + 1}}) ... (x_ {i} -x_ {n})}.$ Pentru j diferit de i , E i este divizibil cu R j , astfel încât E i ≡ 0 modulo R j . Mai mult, modulo R i , X ≡ x i , astfel încât E i ≡ 1 modulo R i .

Pentru orice elemente n + 1 y 0 , y 1 ,…, y n din K , spunând că un polinom P este astfel încât P ( x i ) = y i pentru tot i , este echivalent cu a spune că P ≡ y i modul R eu . Un astfel de polinom P este dat de $P = \ sum _ {{i = 0}} ^ {n} y_ {i} E_ {i},$ care poate fi verificat printr-un calcul direct.

În organismele cu evaluări independente

Teorema restului chinezesc se extinde în mai multe moduri la organismele dotate cu un anumit număr de evaluări independente (a se vedea []). Se găsește apoi sub denumirea de „teoremă de aproximare slabă”:

Fie v 1 , v 2 , ... v n n evaluări discrete independente ale unui câmp K , a 1 , a 2 , ... a n n elemente ale lui K și k 1 , k 2 , ..., k n n numere întregi relative. Atunci există x ∈ K astfel încât v i ( x - a i ) = k i pentru tot i .

Dacă de exemplu K este câmpul numerelor raționale și v i sunt n evaluări p i -adice standard, vedem că această teoremă este un caz special al teoremei restului chinezesc, făcând n i = p i k i (cu notații de la începutul articolului).

Teorema rămâne adevărată pentru evaluările nediscrete, prin înlocuirea k i cu elemente ale grupului de valori ale lui v i (vezi ref. Cit.).

Rezultat pentru inele generale

Dacă R este un inel și I 1 , ..., I k sunt idealuri bilaterale ale lui R două până la două prime între ele (ceea ce înseamnă că I i + I j = R când i ≠ j ), dovedim (prin inducție pe k ) decât morfismul

${\ begin {matrix} R / (I_ {1} \ cap \ cdots \ cap I_ {k}) & \ longrightarrow & R / I_ {1} \ times \ cdots \ times R / I_ {k} \\ x \ ; {\ mathrm {mod}} \, I_ {1} \ cap \ cdots \ cap I_ {k} & \ longmapsto & (x \; {\ mathrm {mod}} \, I_ {1}, \ cdots, x \; {\ mathrm {mod}} \, I_ {k}) \ end {matrix}}$

este un izomorfism și că intersecția ideală a acestor idealuri este egală cu suma tuturor produselor lor în orice ordine:

I_ {1} \ cap \ cdots \ cap I_ {k} = \ sum _ {{\ sigma \ in {\ mathfrak S} _ {k}}} I _ {{\ sigma (1)}} \ cdots I _ {{\ sigma (k)}}.

Dacă inelul este comutativ, toate aceste produse sunt egale, iar intersecția lui I i este pur și simplu egală cu produsul lor. Dar dacă nu este așa, pentru două idealuri bilaterale I și J se primează între ele, în general , și avem doar , de aici și expresia de mai sus, cu o sumă indexată de grupul simetric . $I \ cap J \ neq IJ$ $I \ cap J = IJ + JI$

Aplicații

Aplicațiile teoremei restului chinezesc se găsesc în ramura diofantină a teoriei congruenței.

Următoarea teoremă poate fi privită fie ca o aplicație a teoremei rămășiței chineze, fie ca o generalizare a acestei teoreme.

Fie P i ( x 1 , x 2 , ..., x n ) ≡ 0 mod m i ( i = 1,2, ... k) un sistem de k congruențe, unde P i sunt polinoame ale n variabile , și unde modulele m i sunt perechi prime. Atunci aceste congruențe sunt solvabile în comun dacă și numai dacă fiecare dintre ele este separat solvent; mai exact, dacă m este produsul modulelor m i , fiecare n-tuplu ( x 1 , x 2 , ..., x n ) unde x i este o soluție a congruenței i, determină bijectiv un n- tuplu ( y 1 , y 2 , ..., y n ) modul m satisfacând toate congruențele în același timp.

Mai mult, dacă cineva este de acord să numim „primitivă” o soluție ( x 1 , x 2 , ..., x n ) a unei congruențe astfel încât fiecare dintre x i să fie prim cu modulul m i , atunci teorema anterioară rămâne adevărat dacă îl restrângem la soluții primitive: Congruențele sunt rezolvabile în mod primitiv în comun dacă și numai dacă fiecare dintre ele este separat și există o bijecție între n-tupluri ale soluțiilor primitive modulo m i și cele ale soluțiilor primitive comune modulo m .

Dovada acestei teoreme este simplă: o soluție comună induce în mod evident o soluție pentru fiecare ecuație separat și invers, din astfel de soluții, reconstituim o soluție comună cu teorema restului chinez.

Evident, dacă P i ( x ) = x - a i , vom găsi teoremele restului chinezesc.

O altă teoremă notorie este următoarea:

Fie P ( x 1 , x 2 , ..., x n ) ≡ 0 mod m o congruență, unde P este un polinom al n variabile și să presupunem că m este produsul k modulelor m i prime două câte două. Atunci această congruență este solventă (resp. În principal solvent) modulo m dacă și numai dacă este solvent (resp. În principal solvent) modulo fiecare m i . Din nou, există o bijecție între soluțiile primului modul de congruență m și k-tupluri ale soluțiilor de modul de congruență fiecare m i . Dovada este similară cu cea a teoremei anterioare.

Datorită acestei ultime teoreme, soluția unui modul de congruență m este redusă la cea a soluțiilor modulo fiecare dintre puterile maxime ale factorilor primi care compun m .

Dintre numeroasele aplicații ale teoremei restului chinez la teoria numerelor, să cităm și dovada multiplicativității indicatorului Euler .

O metodă conexă

Am văzut că una dintre aplicațiile majore ale teoremei restului chinezesc rezida în faptul că rezoluția unui modul de congruență un număr m , produs de două numere m 1 și m 2 , se reduce la rezoluția acelui modulo de congruență m 1 și m 2 , când m 1 și m 2 sunt coprimă. De obicei, m i sunt puteri ale unui număr prim, teorema chineză fiind împinsă cât mai departe posibil. Acest lucru simplifică deja mult problemele teoretice și practice, dar cum să reduceți întrebarea și mai mult? Următoarea tehnică este deja utilizată de Gauss în Disquisitiones arithmeticae . Practicat cu pricepere, cel mai adesea prin intermediul unei descendențe infinite , permite o analiză fină a cazurilor în care numerele m 1 și m 2 nu sunt prime între ele și să aducă întrebarea în cele din urmă la modulele prime.

Fie P ( x 1 , x 2 , ..., x n ) ≡ 0 mod m o congruență, unde P este un polinom al n variabile, iar m este produsul lui m 1 și m 2 , nu neapărat prim între ele . Rezoluția acestei congruențe este echivalentă cu rezoluția succesivă a lui P ( x ' 1 , x' 2 , ..., x ' n ) mod 0 mod m 1 , apoi a lui Q ( x " 1 , x" 2 , .. ., x " n ) ≡ 0 mod m 2 , unde polinomul Q cu coeficienți întregi este egal cu

{\ displaystyle Q (X_ {1}, \ ldots, X_ {n}) = {1 \ peste m_ {1}} P (m_ {1} X_ {1} + x '_ {1}, \ ldots, m_ {1} X_ {n} + x '_ {n}).}

Demonstrație

Dacă propoziția are o soluție ( x i ) modulul m , atunci această soluție este evident o soluție modulul m 1 . Prin urmare, putem seta x i = x ' i + m 1 x " i , unde ( x' i ) este o soluție a modulului propus m 1 , iar x" i este un număr întreg determinat de x ' i și x i . Astfel, x " i verifică R ( x" i ) = 0 mod m , cu R = P ( x ' i + m 1 X i ) . Dar este ușor de văzut că toți coeficienții polinomului R sunt multipli ai lui m 1 . Prin urmare, putem simplifica această ultimă congruență cu m 1 , care dă Q ( x " i ) = 0 mod m 2 (notații ale enunțului).

Invers, să presupunem că există o soluție de congruență P ( x ' i ) = 0 mod m 1 și un alt congruență Q ( x " i ) = 0 mod m 2 . Q fiind definit de P și ( x' i ) ca înainte Apoi, ridicând argumentul anterior, vedem că ( x i = x ' i + m 1 x " i ) este o soluție a celui propus.

Utilizări

Teorema restului chinezesc este utilizată pe scară largă în aritmetică și algebră, în special în forma sa generală în aritmetica câmpurilor, atât în demonstrații teoretice, cât și în cazuri practice.

În domeniul algoritmilor, este folosit de exemplu în algoritmul RSA în criptografie și este, de asemenea, implicat în algoritmul Silver-Pohlig-Hellman pentru calcularea logaritmului discret . Este implicat în algoritmul de testare a primăriei Agrawal și Biswas, dezvoltat în 1999.

Permite să reprezinte numere întregi mari ca n-tuple de resturi ale diviziunilor euclidiene. În această formă, operații precum adunarea sau multiplicarea pot fi făcute în paralel în timp constant (fără propagare de transport). Pe de altă parte, comparația sau împărțirea nu sunt banale.

Note și referințe

Potrivit lui A. Zachariou, teorema restul chinez a fost descoperit mai devreme de greci ( Paulo Ribenboim , prim - numere și înregistrări, PUF , 1 st ed., 1994, p. 24 ).
(în) Man Keung Siu, " " Matematică algoritmică "și" Matematică dialectică " ," Proc. 2 d Conferința internațională privind predarea matematicii , 2002, p. 6 .
(The) Leonardus "Pisanus", Liber Abbaci , Tipogr. delle Scienze Matematiche e Fisiche, 1857, p. 304 (S. 311).
(La) L. Euler, " Solutio problematis arithmetici de inveniendo numero, qui per datos numeros divisus relinquat data residua", Commentarii academiae scientiarum Petropolitanae , vol. 7, 1740, p. 46-66 , sau Opera Omnia , seria 1, vol. 2, p. 18-32 .
(La) CF Gauss, Disquisitiones arithmeticae , 1801, p. 23 , §32. Reproducerea traducerii Recherches arithmétiques , Gabay, 1989, p. 15 .
(în) Ulrich Libbrecht, Matematica chineză în secolul al XIII-lea , 1973.
Denis Daumas, Michel Guillemot, Olivier Keller, Raphaël Mizrahi și Maryvonne Spiesser, Teorema restului chinezesc , Texte, comentarii și activități pentru aritmetică în liceu, pe site-ul CultureMath al ENS, § 1. Problema restului Chineză: Întrebări despre originile sale .
Louis Frécon, Aritmetică , Publibook,2016( citiți online ) , p. 121.
(în) Dexter C. Kozen , Theory of Computation , Springer-Verlag, al. "Texte în informatică",2006( ISBN 9781846282973 , citit online ) , p. 86, Prelegere suplimentară B, restul chinezesc
(în) Moshe Jarden , Intersecții ale extensiilor algebrice locale ale unui câmp hilbertian , p. 17, recuzită. 4.4, 4.5 și rmk 4.6. citiți online (articolul nr . 56) .
N. Bourbaki , Algebra , capitolele 1-3 , Springer , 2007 ( ISBN 978-3-540-33849-9 ) p. La I.105 și 103.
Un contraexemplu în inelul matricilor triunghiulare superioare de mărimea 2 este propus în exercițiu în Bourbaki, op. cit. , p. A I.151.
Manindra Agrawal și Somenath Biswas , „ Primality and Identity Testing via Chinese Remaindering ”, Lucrările celui de-al 40-lea Simpozion anual privind fundamentele științei computerelor , IEEE Computer Society, fOCS '99,1999, p. 202– ( ISBN 9780769504094 , citit online , accesat la 9 iulie 2019 )

Vezi și tu

Articole similare

Link extern

(în) Teorema chineză a rămășiței pe tăierea nodului