Teorema lui Brooks
În matematică , în special în teoria graficelor , teorema lui Brooks oferă o relație între gradul maxim al unui grafic conectat nedirecționat și numărul cromatic .
Conform acestei teoreme, într-un grafic în care fiecare vârf are cel mult Δ vecini , vârfurile pot fi colorate cu cel mult Δ culori, fără ca două vârfuri adiacente să aibă aceeași culoare, cu excepția în două cazuri, graficele complete și graficele impare cicluri de lungime, care necesită Δ + 1 culori.
State
Teorema - În orice grafic G nedirectat de grad maxim Δ, numărul cromatic χ (G) satisface χ (G) ≤ Δ, cu excepția cazului în care G este un grafic complet sau un ciclu de lungime impar, caz în care χ (G) = Δ + 1.
Istorie și fundal
Teorema este numită după R. Leonard Brooks , care a publicat o dovadă a acesteia în 1941. Colorarea cu numărul de culori descrisă de teorema lui Brooks este uneori numită colorare Brooks sau colorare Δ- . László Lovász a dat o dovadă mai simplă a teoremei în 1975.
Nu este foarte greu de arătat că, pentru orice grafic, χ (G) ≤ Δ + 1. Într-adevăr, orice vârf v are cel mult Δ vârfuri învecinate, care în cel mai rău caz sunt toate colorate diferit. Chiar și în acest caz, putem lua întotdeauna culoarea (Δ + 1) pentru a v . Meritul lui Brooks a fost acela de a reduce această creștere cu 1 unitate în majoritatea cazurilor.
Demonstrație
Există mai multe dovezi ale teoremei lui Brooks. De exemplu, putem argumenta prin inducție asupra numărului de vârfuri ale graficului. Următoarea demonstrație se desfășoară diferit, se bazează pe algoritmul lacom pentru colorarea graficelor și, prin urmare, are meritul de a furniza algoritmi pentru colorarea graficului (este o demonstrație constructivă ).
Această demonstrație a fost prezentată de Ross Churchley în 2010 pe baza lucrării lui John Adrian Bondy în 2003. Finalul înlocuiește raționamentul lui Bondy cu alte lucrări, astfel încât să nu trebuiască să apeleze mai întâi la rezultatele referitoare la arborii din zona de adâncime .
În cele ce urmează, examinăm succesiv patru cazuri:
- grafice neregulate;
- grafice obișnuite neconectate;
- grafice regulate conectate cu un grad mai mic de 3;
- grafice regulate conectate biconectate de grad mai mare sau egal cu 3.
Cazul graficelor neregulate
Principiul, în cazul graficelor neregulate , este de a ordona vârfurile într-un anumit mod și apoi de a le colora unul după altul folosind algoritmul lacom .
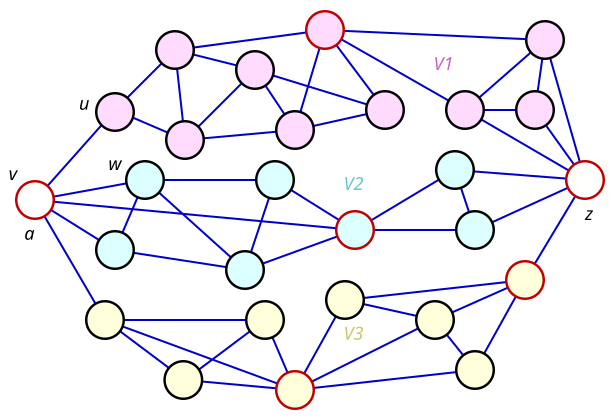
Fie G un grafic neregulat cu n vârfuri și grad maxim Δ. Deoarece G nu este regulat, există cel puțin un vârf x de grade s strict mai mic decât Δ. Plasăm acest vârf la sfârșitul planificării, adică v n = x (figura 1) . Vârfurile adiacente lui x sunt plasate chiar înainte în această ordonare, adică în v n-s , v n-s-1 , ..., v n-1 (figura 2) .
Luăm apoi în considerare vârfurile adiacente lui v n-1 care nu au fost deja ordonate (figura 3) , apoi cele care sunt adiacente lui v n-2 și care nu au fost încă ordonate și așa mai departe până când le ordonăm pe toate, care este posibil deoarece G este conectat (figura 4) .
În această ordonare (v 1 , v 2 ,…, v n ) , toate vârfurile au cel puțin un vârf adiacent posterior (de indice mai mare), cu excepția vârfului x . În consecință, toate au, cu excepția vârfului x , un număr de vârfuri adiacente anterioare (cu indice inferior) strict mai mic decât Δ. Ultimul vârf x are, de asemenea, prin alegerea sa inițială, un număr de vârfuri adiacente anterioare strict mai mici decât Δ.
Apoi colorăm vârfurile v i unul după altul, pentru i variind de la 1 la n . La fiecare pas, vârful v i nu a fost încă colorat. Vârfurile sale adiacente anterioare, care au fost deja colorate, au un număr maxim de Δ - 1 și, prin urmare, utilizează a fortiori un maxim de Δ - 1 culori. Prin urmare, putem lua pentru noul vârf, în cel mai rău caz, culoarea rămasă dintre Δ (figurile 5-8) .
Cazul graficelor regulate neconectate
Într-un grafic neconectat, există cel puțin un punct de articulare , adică un vârf care, dacă este eliminat, face graficul neconectat.
Luați în considerare un astfel de grafic regulat G al gradului Δ care nu este conectat și să fie x un punct de articulație al lui G (în roșu în figura 1).
Descompunem G prin înmulțirea punctului de articulație ca în FIG. 2. Obținem cel puțin două grafice neregulate conectate de grad maxim Δ: într-adevăr, vârfurile obținute prin înmulțirea x sunt fiecare de grad strict mai mic decât Δ.
Unul este astfel readus în cazul precedent și se poate colora fiecare componentă neconectată conectată utilizând metoda expusă anterior. Putem aranja ca vârfurile obținute prin înmulțirea x să aibă aceeași culoare: pentru aceasta, schimbăm culorile în componentele conectate, dacă este necesar.
Rămâne doar să reasamblați părțile grafului pentru a obține un grafic colorat cu with culori.
Caz de grafice regulate conectate de două grade cu un grad mai mic de 3
Singurul grafic regulat conectat de gradul 0 este graficul 0 regulat compus dintr-un singur vârf. Poate fi colorat cu 1 culoare (figura 1) . Întrucât se încadrează în categoria graficelor complete, satisface afirmația teoremei lui Brooks.
Singurul grafic regulat conectat de 1 grad este graficul 1 regulat format din doar două vârfuri, cu o margine între aceste două vârfuri (figura 2) . Poate fi colorat cu 2 culori și și aici suntem în cazul unui grafic complet: satisface afirmația teoremei lui Brooks.
Singurele grafice regulate conectate de gradul 2 sunt cicluri. Ciclurile cu un număr par de vârfuri pot fi colorate cu 2 culori (figura 4) și sunt necesare 3 culori pentru ciclurile cu un număr impar de vârfuri (figurile 3 și 5) . În ambele cazuri, afirmația teoremei lui Brooks susține.
Cazul graficelor regulate de legătură biconectate de grad mai mare sau egal cu 3
Dacă graficul G este complet și de grad Δ, are Δ + 1 vârfuri pe care le putem colora fiecare cu o culoare diferită. Și în acest caz se menționează afirmația teoremei lui Brooks.
Dacă graficul nu este complet, vom comanda din nou un anumit număr de vârfuri, apoi le vom colora folosind algoritmul lacom. Cu toate acestea, nu este la fel de simplu ca în cazul graficului neregulat, deoarece nimic nu garantează a priori să avem o culoare liberă când ajungem la ultimul vârf. Prin urmare, vom aranja ca ultimul vârf colorat v să aibă doi vecini u și w deja colorați în aceeași culoare, ceea ce ne asigură că vom avea cel puțin încă o culoare liberă atunci când vine vorba de colorarea v .
Fie G un grafic necomplet, biconectat, de grad Δ ≥ 3. Există trei vârfuri u , v și w astfel încât
- u este conectat la v ;
- v este conectat la w ;
- dar u nu este conectat la w .
Deoarece G nu este complet, există două vârfuri a și b care nu sunt legate direct de o margine. Pe măsură ce graficul este conectat, există o cale ( a , v 1 , v 2 , ..., v p , b ) care leagă a la b . Fie eu cea mai mare valoare astfel încât v i să aibă legătură cu a . Se consideră u = a , v = v i și w = v i + 1 . Aceste trei vârfuri verifică dacă u și w sunt legate de v fără a fi legate între ele.
Deoarece graficul este biconectat, putem elimina u sau w din acesta fără a înceta să fim conectați: G - { u } și G - { w } sunt conectați. Putem chiar reuși să luăm u , v și w astfel încât G - { u , w } să fie încă conectat.
Demonstrație Lema 2 Într-un grafic biconectat G, de grad minim 3 sau mai mult și care nu este complet, putem găsi vârfurile u și w învecinate cu același vârf v , dar nu învecinate între ele, astfel încât G - { u , w } este încă conectat.Deoarece graficul nu este complet, există cel puțin un vârf a care nu este adiacent tuturor celorlalte.
Dacă G - { a } este biconectat, luăm, ca în dovada Lemei 1, u = a și w egală cu orice vârf la distanța 2 de a . Deoarece G - { a } este conectat, putem elimina w din acesta fără a pierde conectivitatea, iar G - { u , w } este conectat.
Luați în considerare acum cazul în care G - { a } este conectat, dar nu biconectat. Prin urmare, are puncte de articulare (în roșu în figură) . Fie z unul dintre aceste puncte de articulare. G - { a , z } nu este conectat, este chiar împărțit în cel puțin două componente conectate disjuncte. Fiecare dintre aceste componente conectate V 1 , V 2 ,… V n poate fi la rândul său tăiată în componente biconectate conectate prin punctele de articulație. Aceste componente biconectate formează un copac cu rădăcina z .
În G, a are un vecin în fiecare dintre frunze la capătul acestui copac. Într-adevăr, dacă eliminăm punctul de articulație z i de care este atașată frunza, dacă nu ar fi conectat la a la celălalt capăt, G - { z i } ar fi neconectat, ceea ce este imposibil, deoarece G este biconectat.
Să luăm u în una dintre frunze la sfârșitul lui V 1 și w într-una din frunze la sfârșitul lui V 2 și să v = a . Vârfurile u și w sunt foarte apropiate de v . Nu sunt adiacente, deoarece sunt luate din diferite componente conectate.
Vârfurile u și w fiind luate în componente biconectate ale lui G - { a } în timp ce sunt diferite de punctele de articulare ale lui G - { a }, G - { a , u , w } rămâne conectat. După cum, de altfel, gradul de o mai mare sau egal cu 3, există un al treilea nod care permite să se conecteze un G - { a , u , w }. Prin urmare, graficul G - { u , w } este conectat.
Deoarece G - { u , w } este conectat, îl putem comanda ca în cazurile anterioare dând v cel mai puternic număr. Apoi colorăm G după cum urmează:
- colorăm u și w cu aceeași culoare, ceea ce este posibil deoarece nu sunt conectate (figura 1) ;
- apoi colorăm restul graficului respectând ordinea pe care tocmai am stabilit-o. Deoarece fiecare dintre vârfuri, cu excepția ultimului, are cel puțin un vecin necolorat, are cel mult Δ - 1 vecini colorate și poate fi colorat rămânând în within culorile impuse.
Când ajungem să colorăm ultimul vârf v , avem garanția că rămâne o culoare liberă, deoarece cei doi vecini ai săi u și w au aceeași culoare (figura 2) .
Rezultate învecinate
O generalizare a teoremei lui Brooks se aplică colorării listelor : dat un grafic nedirecționat și conectat de grad maxim Δ care nu este nici un grafic complet, nici un ciclu de lungime impar și o listă de list culori pentru fiecare vârf, este posibil să alegeți un culoare pentru fiecare vârf luat în lista sa, astfel încât două vârfuri adiacente să nu aibă niciodată aceeași culoare. Cu alte cuvinte, numărul cromatic al listei unui grafic conectat nedirecționat nu este niciodată mai mare de Δ, cu excepția cazului unui grafic complet sau a unui ciclu de lungime impar. Acest lucru a fost demonstrat de Vadim Vizing în 1976.
Cu unele grafice, avem nevoie chiar de mai puține Δ culori. Bruce Reed arată că Δ - 1 culori sunt suficiente dacă și numai dacă graficul nu are Δ- clicuri când Δ este suficient de mare. Pentru graficele fără triunghi (fără un set de trei vârfuri adiacente în perechi), sau mai general pentru graficele în care vecinătatea fiecărui vârf este suficient de goală , culorile O (Δ / log Δ) sunt suficiente.
Gradul unui grafic apare și în limitele superioare ale numărului de culori necesare pentru alte tipuri de colorare:
- în colorarea marginilor unui grafic , rezultatul conform căruia indicele cromatic este mai mic sau egal cu Δ + 1 este teorema Vizing ;
- o extensie a teoremei lui Brooks la colorarea totală (en) a unui grafic care afirmă că numărul cromatic total este cel mult Δ + 2, a fost conjecturată de Behzad și Vizing;
- teorema Hajnal- Szemerédi privind colorarea echitabilă a unui grafic afirmă că orice grafic poate fi colorat cu cel mult Δ + 1 culori, astfel încât numărul de vârfuri ale fiecărei culori să difere cel mult cu 1.
Algoritmi
O colorare cu Δ culori, sau chiar o colorare prin listă cu Δ culori, a unui grafic de grad maxim Δ poate fi obținută într-un timp liniar (proporțional cu numărul de vârfuri și margini). Sunt cunoscuți, de asemenea, algoritmi eficienți care fac posibilă găsirea petelor Brooks folosind prelucrări paralele sau distribuite.
Note și referințe
- (în) RL Brooks , „ colorează nodurile unei rețele ” , Proc. Cambridge Philosophical Society, Math. Fizic. Știință. , vol. 37,1941, p. 194-197 ( citește online ).
- (în) L. Lovász , „ Trei probe scurte în teoria graficelor ” , J. Combin. Th., Seria B , vol. 19,1975, p. 269–271 ( DOI 10.1016 / 0095-8956 (75) 90089-1 )
- (în) Ross Churchley, " Teoria graficului haiku - Trei scurte și dovezi frumoase ", noiembrie 2010.
- (în) JA Bondy , „ Scurte dovezi ale teoremelor clasice ” , Journal of Graph Theory , vol. 44, n o 3,noiembrie 2003, p. 159 până la 165
- (în) Bradley Baetz și David R. Wood, „ Brooks Vertex-Coloring Theorem in Linear Time , Raport tehnic CS-AAG-2001-05, Universitatea din Sydney, octombrie 2001.
- (în) Dieter Jungnickel, „ Graphs, Networks and Algorithms ”, volumul 5, ediția a doua, Springer Verlag, mai 2003 ( ISBN 3-540-63760-5 ) .
- (ru) VG Vizing , „ Vertex colorings with given colors ” , Diskret. Analiz. , vol. 29,1976, p. 3-10
- (în) Bruce Reed , „ O întărire a teoremei lui Brooks ” , J. Combin. Th., Seria B , vol. 76, n o 21999, p. 136–149 ( DOI 10.1006 / jctb.1998.1891 )
- (în) Noga Alon Michael Krivelevich și Benny Sudakov , „ Colorarea graficelor cu cartiere rare ” , J. Combin. Th., Seria B , vol. 77, n o 1,1999, p. 73–82 ( DOI 10.1006 / jctb.1999.1910 )
- (în) San Skulrattanakulchai , „ Δ-List vertex colorating in linear time ” , Inf. Proces. Lett. , vol. 98, n o 3,2006, p. 101–106 ( DOI 10.1016 / j.ipl.2005.12.007 )
- (în) HJ Karloff , „ Un algoritm pentru teorema NC Brooks ” , TCS , vol. 68, n o 1,1989, p. 89–103 ( DOI 10.1016 / 0304-3975 (89) 90121-7 )
- (în) Péter Hajnal și Endre Szemerédi , " Brooks colorare în paralel " , SIAM J. Discrete Math. , vol. 3, n o 1,1990, p. 74–80 ( DOI 10.1137 / 0403008 )
- (în) Alessandro Panconesi și Aravind Srinivasan , " The local kind of Δ-colouring and its algorithmic applications " , combinatorica , vol. 15, n o 21995, p. 255–280 ( DOI 10.1007 / BF01200759 )
- (în) David A. Grable și Alessandro Panconesi , „Algoritmi rapizi pentru colorări distribuite Brooks-Vizing” în SODA '98: Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms , Philadelphia, PA, SUA, SIAM , al. „Journal of Algorithms” ( nr . 37),1998( DOI 10.1006 / jagm.2000.1097 , citiți online )
Link extern
(ro) Eric W. Weisstein , „ Brooks 'Theorem ” , pe MathWorld