Algoritmul lui Dijkstra

Algoritmul lui Dijkstra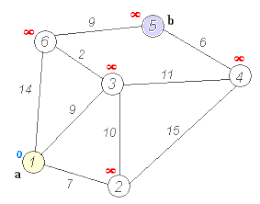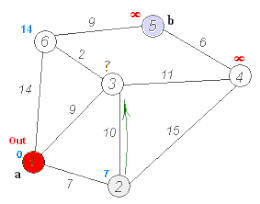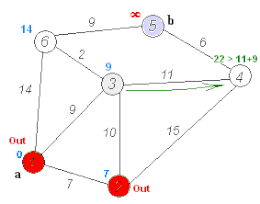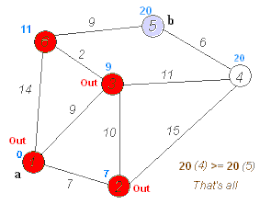 pentru găsirea celei mai scurte căi între a și b. Alege vertexul nevizitat cu cea mai mică distanță, calculează distanța prin el până la fiecare vecin nevizitat și actualizează distanța vecinului dacă este mai mică. Marcează vârful vizitat (în roșu) când a terminat cu vecinii.

Descoperitor sau inventator	Edsger Dijkstra
Data descoperirii	1959
Probleme similare	Algoritmul de căutare a căii ( d ) , algoritmul teoriei graficelor ( d ) , algoritm lacom , algoritm
Structură de date	Grafic
Bazat pe	Algoritm de traversare a lățimii
La inceputul	Algoritmul A * , protocolul de rutare a statului de legătură ( en ) , Deschideți cea mai scurtă cale mai întâi , IS-IS

Complexitatea timpului

Cel mai rău caz	${\ displaystyle O (\| E \| + \| V \| \ log \| V \|)}$ , ${\ displaystyle O (\| E \| + \| V \| \ log \| V \|)}$

În teoria graficelor , algoritmul Dijkstra (pronunțat [dɛɪkstra] ) este utilizat pentru a rezolva cea mai scurtă problemă de cale . Permite, de exemplu, să se determine o cale mai scurtă pentru a merge dintr-un oraș în altul, cunoscând rețeaua rutieră a unei regiuni. Mai precis, calculează cele mai scurte căi de la o sursă la toate celelalte vârfuri într-un grafic direcționat ponderat de reali pozitivi. Poate fi, de asemenea, utilizat pentru a calcula o cale mai scurtă între un vârf de pornire și un vârf de final.

Algoritmul poartă numele inventatorului său, informaticianul olandez Edsger Dijkstra și a fost publicat în 1959.

Acest algoritm este de complexitate polinomială . Mai precis, pentru vârfuri și arce, timpul este în sau chiar în . $nu$ $la$ ${\ displaystyle O ((a + n) \ log n)}$ ${\ displaystyle O (a + n \ log n)}$

Cea mai scurtă problemă de cale

Algoritmul lui Dijkstra rezolvă o problemă algoritmică : cea mai scurtă problemă de cale . Această problemă are mai multe variante. Cel mai simplu este următorul: dat un grafic nedirecționat , ale cărui margini sunt prevăzute cu greutăți și două vârfuri ale acestui grafic, găsiți o cale între cele două vârfuri din grafic, cu greutate minimă. Algoritmul lui Dijkstra face posibilă rezolvarea unei probleme mai generale: graficul poate fi orientat și putem desemna un vârf unic și putem cere lista celor mai scurte căi pentru toate celelalte noduri ale graficului.

Principiu pe un exemplu

Algoritmul ia ca intrare un grafic direcționat ponderat de reali pozitivi și un vârf sursă. Aceasta implică construirea progresivă a unui subgraf în care diferiții vârfuri sunt clasificate în ordinea crescătoare a distanței lor minime față de vârful de pornire. Distanța corespunde sumei greutăților arcurilor împrumutate.

Inițial, considerăm că distanțele de la fiecare vârf la vârful de pornire sunt infinite, cu excepția vârfului de pornire pentru care distanța este zero. Subgraful de pornire este setul gol.

În timpul fiecărei iterații, alegem în afara subgrafului un vârf de distanță minimă și îl adăugăm la subgraf. Apoi, actualizăm distanțele vârfurilor vecine ale celui adăugat. Actualizarea se efectuează după cum urmează: noua distanță față de vârful vecin este minima dintre distanța existentă și cea obținută prin adăugarea greutății arcului între vârful vecin și vârful adăugat la distanța de la vârful adăugat.

Continuăm în acest mod până când vârfurile sunt epuizate (sau până când este selectat vârful de sosire).

Distanța dintre orașul A și orașul J

Algoritmul lui Dijkstra funcționează și pe un grafic nedirecționat (care poate face mai mult poate face mai puțin). Exemplul opus arată pașii succesivi în rezolvarea celei mai scurte căi dintr-un grafic. Nodurile simbolizează orașele identificate printr-o literă, iar crestele indică distanța dintre aceste orașe. Încercăm să determinăm cea mai scurtă rută pentru a merge din orașul A în orașul J.

În nouă etape, putem determina cea mai scurtă cale care duce de la A la J, trece prin C și H și are o lungime de 487 km .

Prezentare sub formă de tabel

De asemenea, putem rezuma execuția algoritmului lui Dijkstra cu o matrice. Fiecare pas corespunde unei linii. O linie oferă vârfurile curente distanțe față de vârful de pornire. O coloană oferă evoluția distanțelor unui vârf dat de vârful de pornire în timpul algoritmului. Distanța de la un vârf ales (deoarece minimă) este subliniată. Distanțele actualizate sunt tăiate dacă sunt mai mari decât distanțele deja calculate.

Algoritmul lui Dijkstra

	la A	la B	la C	la D	la E	la F.	la G	la H	avea	la J
pasul inițial	0	∞	∞	∞	∞	∞	∞	∞	∞	∞
A (0)		85	217	∞	173	∞	∞	∞	∞	∞
B (85 A )		-	217	∞	173	165	∞	∞	∞	∞
F (165 B )		-	217	∞	173	-	∞	∞	415	∞
E (173 A )		-	217	∞	-	-	∞	∞	415	675
C (217 A )		-	-	∞	-	-	403	320	415	675
H (320 C )		-	-	503	-	-	403	-	415	675 487
G (403 C )		-	-	503	-	-	-	-	415	487
I (415 F )		-	-	503	-	-	-	-	-	487
J (487 H )		-	-	503	-	-	-	-	-	-
D (503 M )		-	-	-	-	-	-	-	-	-

Tabelul oferă nu numai distanța minimă de la orașul A la orașul J (487), ci și calea înapoi (J - H - C - A) pentru a merge de la A la J, precum și toate distanțele minime de la orașul A la celelalte orașe enumerate în ordine crescătoare.

Diagrama algoritmului

Graficul este notat unde: $G = (S, A)$

mulțimea este mulțimea finită a vârfurilor grafului ; $S$ $G$
setul este setul de arcuri de astfel încât: dacă este în , atunci există un arc de la nod la nod ; $LA$ $G$ $(s_ {1}, s_ {2})$ $LA$ $s_ {1}$ $s_ {2}$
definim funcția definită în care un cuplu asociază greutatea pozitivă a arcului care se conectează la (și dacă nu există niciun arc care se conectează la ). ${\ displaystyle weight}$ $S \ ori S$ ${\ displaystyle \ mathbb {R} ^ {+} \ cup \ {+ \ infty \}}$ $(s_ {1}, s_ {2})$ $greutate (s_ {1}, s_ {2})$ $s_ {1}$ $s_ {2}$ $+ \ infty$ $s_ {1}$ $s_ {2}$

Greutatea căii dintre două vârfuri este suma greutăților arcurilor care o compun. Pentru o pereche dată de vârfuri (vârful de pornire) (vârful de sosire) aparținând , algoritmul găsește o cale de la până la cu o greutate mai mică (cu alte cuvinte o cale mai ușoară sau chiar cea mai scurtă). $s _ {{deb}}$ $s _ {{end}}$ $S$ $s _ {{deb}}$ $s _ {{end}}$

Algoritmul funcționează prin construirea unui subgraf astfel încât distanța dintre un vârf în de la este cunoscută și este minimă în . Inițial, conține doar nodul izolat, iar distanța de la el însuși este zero. Arcurile sunt adăugate la fiecare pas: $P$ $s$ $P$ $s _ {{deb}}$ $G$ $P$ $s _ {{deb}}$ $s _ {{deb}}$ $P$

1. prin identificarea tuturor arcurilor din ;

a_ {i} = (s_ {i1}, s_ {i2})

P \ ori G

2. prin alegerea arcului în care se dă distanța minimă de la până la trecerea tuturor căilor create care duc la acest nod.

a_ {j} = (s_ {j1}, s_ {j2})

P \ ori G

s _ {{deb}}

s _ {{j2}}

Algoritmul de capete , fie atunci când devine un arbore de acoperire a , sau atunci când toate nodurile de interes sunt . $P$ $G$ $P$

Prin urmare, putem scrie algoritmul după cum urmează:

Entrées :

G=(S,A)

un graphe avec une pondération positive

poids

des arcs,

s_{{deb}}

un sommet de

S

P:=\emptyset

d[a]:=+\infty

pour chaque sommet

a

d[s_{deb}]=0

Tant qu'il existe un sommet hors de

P

Choisir un sommet

a

hors de

P

de plus petite distance

d[a]

Mettre

a

dans

P

Pour chaque sommet

b

hors de

P

voisin de

a

Si d[b] > d[a] + poids(a, b)

d[b]=d[a]+poids(a,b)

prédécesseur[b] := a Fin Pour Fin Tant Que

Implementarea algoritmului

Funcții auxiliare

Algoritmul folosește următoarele funcții auxiliare.

Inițializarea algoritmului Initialisation(G,sdeb) 1 pour chaque point s de G faire 2 d[s] := infini /* on initialise les sommets autres que sdeb à infini */ 3 fin pour 4 d[sdeb] := 0 /* la distance au sommet de départ sdeb est nulle */ Găsirea unui nod de distanță minimă

Căutăm un nod cu distanță minimă (conectat prin arcul cu cea mai mică greutate) dintre nodurile situate în exterior . Se remarcă complementul . Se implementează pentru aceasta o funcție Trouve_min (Q) care alege un nod de Q de distanță minimă. $s _ {{deb}}$ $P$ $P$ $Î$

Trouve_min(Q) 1 mini := infini 2 sommet := -1 3 pour chaque sommet s de Q 4 si d[s] < mini 5 alors 6 mini := d[s] 7 sommet := s 8 renvoyer sommet Actualizarea distanțelor

Actualizăm distanțele dintre și punând întrebarea: este mai bine să parcurgem sau nu? $s _ {{deb}}$ $s _ {{2}}$ $s _ {{1}}$

maj_distances(s1,s2) 1 si d[s2] > d[s1] + Poids(s1,s2) /* Si la distance de sdeb à s2 est plus grande que */ 2 /* celle de sdeb à S1 plus celle de S1 à S2 */ 3 alors 4 d[s2] := d[s1] + Poids(s1,s2) /* On prend ce nouveau chemin qui est plus court */ 5 prédécesseur[s2] := s1 /* En notant par où on passe */

Functie principala

Iată funcția principală care folosește funcțiile laterale anterioare:

Dijkstra(G,Poids,sdeb) 1 Initialisation(G,sdeb) 2 Q := ensemble de tous les nœuds 3 tant que Q n'est pas un ensemble vide faire 4 s1 := Trouve_min(Q) 5 Q := Q privé de s1 6 pour chaque nœud s2 voisin de s1 faire 7 maj_distances(s1,s2) 8 fin pour 9 fin tant que

Cea mai scurtă cale de la la poate fi apoi calculată iterativ în conformitate cu următorul algoritm, secvența reprezentând cea mai scurtă cale de la la : $s _ {{deb}}$ $s _ {{end}}$ $LA$ $s _ {{deb}}$ $s _ {{end}}$

1 A = suite vide 2 s := sfin 3 tant que s != sdeb faire 4 A = A + s /* on ajoute s à la suite A */ 5 s = prédécesseur[s] /* on continue de suivre le chemin */ 6 fin tant que

Atenție: dacă nu există o cale către această parte a algoritmului este o buclă infinită sau o eroare în funcție de implementarea dvs. $s _ {{deb}}$ $s _ {{end}}$

Specializarea algoritmului

Este posibil să se specializeze algoritmul oprind căutarea atunci când se verifică egalitatea , în cazul în care se caută doar distanța minimă dintre și . $s_ {1} = s_ {end}$ $s _ {{deb}}$ $s _ {{end}}$

Complexitatea algoritmului

Eficiența algoritmului Dijkstra se bazează pe o implementare eficientă a Trouve_min . Întregul este implementat printr-o coadă prioritară . Dacă graficul are arce și noduri, că este reprezentat de liste de adiacență și dacă coada de prioritate este implementată de o grămadă binară (presupunând că comparațiile dintre greutățile arcurilor sunt în timp constant), atunci complexitatea temporală a algoritmului este . Pe de altă parte, dacă implementăm coada prioritară cu o grămadă Fibonacci , algoritmul este în . $Î$ ${\ displaystyle | A |}$ $| S |$ ${\ displaystyle O ((| A | + | S |) \ times \ log (| S |))}$ ${\ displaystyle O (| A | + | S | \ times \ log (| S |))}$

Corectarea algoritmului

Dovada corectării este o reapariție pe Card ( P ) (care crește cu 1 la fiecare iterație) și se bazează pe următorul invariant:

${\ displaystyle {\ begin {cases} \ forall c \ in P, \, d (c) = mini (c) \\\ forall c \ not \ in P, \, d (c) = miniP (c) \ sfârșit {cazuri}}}$

mini ( c ) este greutatea unei căi mai scurte care duce la c ;
miniP ( c ) este greutatea unei căi mai scurte din care toate vârfurile intermediare sunt în P care duc la c .

Dacă n = Card ( P ), dovada este următoarea:

pentru n = 0 și 1: imediat;
pentru n un întreg diferit de zero, să presupunem că invariantul este adevărat.

Algoritmul selectează un pivot astfel încât și îl adaugă în P. Prin urmare, este necesar să se arate că după modificarea lui P: ${\ displaystyle a \ not \ în P}$ ${\ displaystyle d (a) = {\ underset {x \ not \ in P} {Min}} \, d (x)}$ ${\ displaystyle d (a) = mini (a)}$

Prin ipoteză, înainte de modificarea lui P , deci dacă există o cale C astfel încât atunci această cale conține cel puțin un vârf b a astfel încât . ${\ displaystyle d (a) = miniP (a)}$ ${\ displaystyle weight (C) <d (a)}$ ${\ displaystyle \ neq}$ ${\ displaystyle b \ not \ în P}$

Deci, să fie un astfel de vârf b astfel încât toți predecesorii săi din C să fie în P (există pentru că primul vârf al lui C este originea care se află în P ). Descompună C în Cb - și Cb + în cazul în care Cb - este prima parte a C , care este ultimul vârf b , și Cb + După C . Deci : contradicție. ${\ displaystyle weight (C) = greutate (Cb -) + greutate (Cb +) \ geq weight (Cb -) = d (b) \ geq d (a)}$

Prin urmare, nu există o cale C, cum ar fi de unde . Egalitatea este întotdeauna valabil și pentru alte elemente P . ${\ displaystyle weight (C) <d (a)}$ ${\ displaystyle d (a) = mini (a)}$

În cele din urmă, algoritmul pune actualizare funcția de (și predecesorul) pentru succesorii b pivot are : . $d [b] = \ min (d [b], d [a] + greutate (a, b))$

Să arătăm că atunci : ${\ displaystyle \ forall c \ not \ în P, \, d (c) = miniP (c)}$

în cazul în c nu este un succesor al pivotului A , atunci nu există nici o cale nouă C , care să conducă la C , astfel încât și ale căror vârfuri intermediare sunt în P , după adăugarea unui în P , deoarece ar trebui apoi să treacă printr - o înainte de a trece printr - un alt vertex , dar nu ar fi cea mai scurtă cale către d, deoarece greutatea celei mai scurte căi către d a fost deja calculată înainte de a adăuga a la P prin ipoteză și, prin urmare, această cale conține doar vârfuri care au fost în P înainte de adăugarea unui în P ; ${\ displaystyle weight (C) <d (c)}$ ${\ displaystyle d \ în P}$

dacă nu, există astfel de căi, denotând C cel mai bun dintre ele, atunci C va fi una dintre noile căi generate de ingestia pivotului a de către P , prin urmare și pe de altă parte pivotul a este ultimul vârf intermediar al C deoarece cea mai scurtă cale care duce la celelalte vârfuri ale lui P nu trece printr- o așa cum s-a explicat mai sus. Prin urmare, este unirea celei mai scurte căi care duce la a cu arcul ( a , c ): prin urmare . ${\ displaystyle a \ în C}$ ${\ displaystyle weight (C) = d (c) = weight ((a, c)) + d (a) = miniP (c)}$

Aplicații

Algoritmul lui Dijkstra găsește utilitate în calculul rutelor rutiere. Greutatea arcurilor poate fi distanța (pentru cea mai scurtă rută), timpul estimat (pentru cea mai rapidă rută), consumul de combustibil și prețul taxelor (pentru cea mai economică rută).

O aplicație obișnuită a algoritmului lui Dijkstra apare în protocoalele de rutare interne de „stare de legătură”, cum ar fi Open Shortest Path First ( OSPF ) sau IS-IS - sau chiar PNNI (en) pe rețelele ATM -, care permit rutare foarte eficientă a informațiilor prin internet căutând cel mai eficient traseu.

Comparație cu alți algoritmi

Algoritmul lui Dijkstra se bazează pe o cale de lățime .
Specializarea algoritmului lui Dijkstra care calculează o cale mai scurtă de la sursă la destinație este o instanță a algoritmului A * în care funcția euristică este funcția nulă. Algoritmul A * care ar folosi o euristică inferioară și monotonă (de exemplu, distanța pe care o zboară cioara) poate fi mai eficient .
Algoritmul nu se aplică graficelor cu greutăți negative. Dar algoritmul Bellman-Ford rezolvă problema celor mai scurte căi de la o sursă cu greutăți negative (dar fără ciclu negativ).
Floyd-Warshall algoritm Calculează trasee mai scurte între toate nodurile într - un grafic în care ponderile pot fi negative.

Note și referințe

(în) Edsger Dijkstra , „ O notă despre două probleme legate de grafice ” , Numerische Mathematik , Springer Science + Business Media , Vol. 1, n o 1,Decembrie 1959, p. 269-271 ( ISSN 0029-599X și 0945-3245 , OCLC 1760917 , DOI 10.1007 / BF01386390 , citiți online )
" http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.54.4349&rep=rep1&type=pdf "
Dijkstra, EW, „ O notă despre două probleme legate de grafice ”, Numerische Mathematik , vol. 1,1959, p. 269–271 ( DOI 10.1007 / BF01386390. ).
De exemplu, nodurile care nu au alte margini decât cea pe care a traversat-o pentru a ajunge la ele, nu sunt considerate noduri de interes.
Șirul / * ... * / este un comentariu .
Cormen și colab. 2010 , p. 610
(în) John Moy, " RFC2328 OSPF Versiunea 2 " ,Aprilie 1998(accesat la 19 mai 2016 ) :„ Folosind algoritmul Dijkstra, se formează un arbore din acest subset al bazei de date a stării legăturilor. »,P. 161
(în) David R. Oran " RFC1142: Protocol de rutare intra-domeniu OSI IS-IS " ,Februarie 1990(accesat la 19 mai 2016 ) :„ Un algoritm inventat de Dijkstra (vezi referințele) cunoscut sub numele de cea mai scurtă cale (SPF), este folosit ca bază pentru calcularea rutei. "

Anexe

Bibliografie

(ro) „ O scurtă introducere în arta programării ” de Edsger W. Dijkstra , 1971, conținând articolul original (1959) care descrie algoritmul lui Dijkstra (paginile 67-73).
(ro) Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest și Clifford Stein , Introducere în algoritmi , MIT Press și McGraw-Hill ,2001, A 2 -a ed. [ detaliul ediției ], secțiunea 24.3, „ Algoritmul lui Dijkstra ”, paginile 595–601.
Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest și Clifford Stein ( trad. Din engleză), Algoritmi : Prelegere cu exerciții 957 și 158 probleme , Dunod ,2010[ detaliul ediției ]

Articole similare

Glosar al teoriei graficelor
Găsirea căilor și problemele căii
Algoritm de traversare a lățimii
Algoritmul A *
Articol despre algoritmul Ford-Bellman care calculează cea mai scurtă cale cu greutăți negative ale arcului

Algoritmul lui Dijkstra

Cea mai scurtă problemă de cale

Principiu pe un exemplu

Distanța dintre orașul A și orașul J

Prezentare sub formă de tabel

Diagrama algoritmului

Implementarea algoritmului

Funcții auxiliare

Functie principala

Specializarea algoritmului

Complexitatea algoritmului

Corectarea algoritmului

Aplicații

Comparație cu alți algoritmi

Note și referințe

Anexe

Bibliografie

Articole similare

linkuri externe